Оглавление:
Правила дифференцирования существенно расширяют возможности практического нахождения производных. Однако наиболее мощным средством нахождения производных является правило дифференцирования сложных функций.
Рассмотрим функции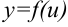 
и 
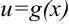. Тогда функция 
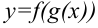будет называться сложной функцией. Например, если 
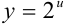, а 
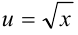, то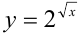 
будет являться сложной функцией.
Для нахождения производной сложной функции будем использовать следующую теорему: если функция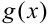 
дифференцируема по переменной 
, а функция 
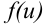дифференцируема по переменной 
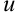, то сложная функция 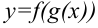дифференцируема по переменной , причем её производная вычисляется по формуле: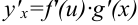 
.
Функцию 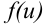называют основной функцией, a 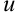— «сложностью». Тогда правило нахождения производной сложной функции будет иметь вид: производная сложной функции равна производной основной функции, умноженной на производную «сложности»: 
.
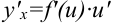При нахождении производных конкретных функций целесообразно принимать какое-либо выражение за 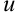, чтобы прийти к одной из следующих формул дифференцирования сложных функций:
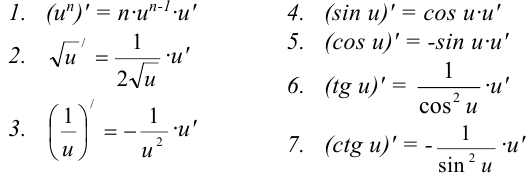
Рассмотрим нахождение производных сложных функций на конкретных примерах.
Пример №11.5.
Найдите производную функции .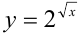
Решение:
Функция 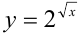— сложная функция. Обозначим 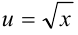и придем к показательной функции 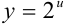. Найдем ее производную по таблице производных сложных функций:
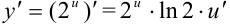. Заменяя 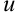через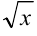 
придем к производной вида:
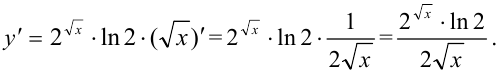
Ответ: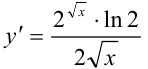 
Пример №11.6.
Найдите производную функции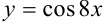 
.
Решение:
Функция 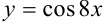— сложная функция. Обозначим 
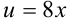и придем к тригонометрической функции 
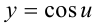. Найдем ее производную по таблице производных сложных функций:
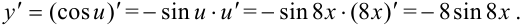
Ответ: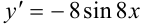 
Пример №11.7.
Найдите производную функции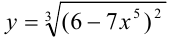 
.
Решение:
Представим исходную функцию в виде степени: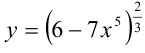 
. Обозначим 
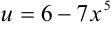и придем к функции 
.
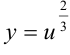Тогда
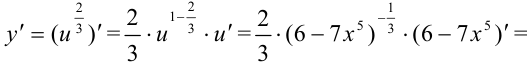
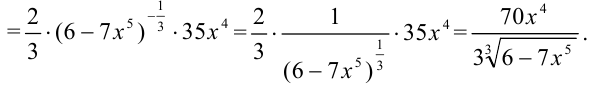
Ответ: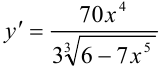 
Пример №11.8.
Найдите производную функции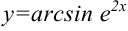 
.
Решение:
Обозначим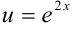 
и придем к функции 
.
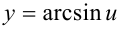Тогда
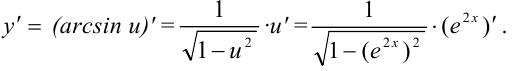
Видим, что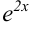 
тоже сложная функция, обозначив 
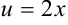, найдем её производную:
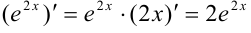(здесь мы применили краткую запись решения).
Получили,что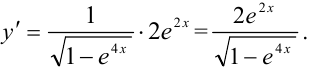 
Ответ: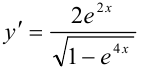 
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Нахождение производных основных элементарных функций. |
| Правила дифференцирования функций. |
| Геометрический смысл производной. |
| Уравнение касательной к кривой. |
