Для нахождения производных основных элементарных функции по определению будем использовать схему, рассмотренную выше. Приведем пример нахождения производной функции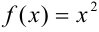 
.
Пример №11.1.
Найдите производную функции 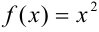в произвольной, но фиксированной точке 
.
Решение:
1. Дадим аргументу приращение 
.
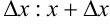2. Найдем соответствующее приращение функции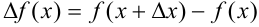 
: 
.
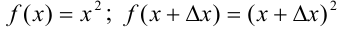Тогда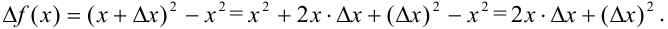 
3. Составим отношение приращения функции к приращению аргумента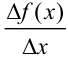 
: 
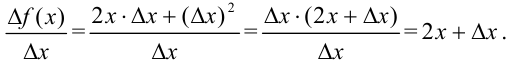
4. Найдем предел этого отношения при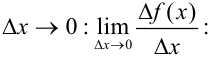 
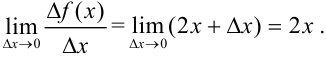
Поскольку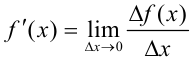 
, то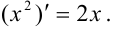 
Ответ: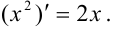
Аналогично выводятся формулы нахождения всех производных основных элементарных функций. Приведем их: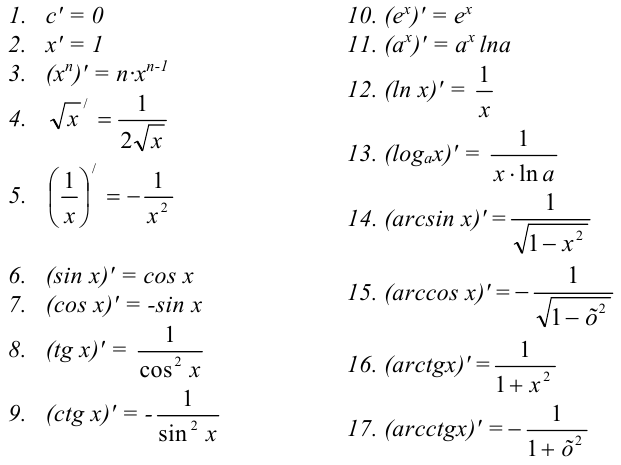
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Точки разрыва, их классификация. |
| Понятие производной функции. |
| Правила дифференцирования функций. |
| Производная сложной функции. |
