Имеют место следующие теоремы о непрерывных функциях:
Теорема 2.1. Пусть функции 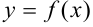 и
и 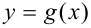 непрерывны в точке
непрерывны в точке  . Тогда
. Тогда
- сумма или разность
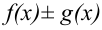 непрерывны в точке
непрерывны в точке  ;
; - произведение
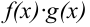 непрерывно в точке
непрерывно в точке  ;
; - при дополнительном условии
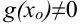 частное
частное 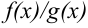 также непрерывно в точке
также непрерывно в точке  .
.
Теорема 2.2. Пусть функция 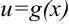 непрерывна в точке
непрерывна в точке  , а функция
, а функция 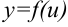 непрерывна в точке
непрерывна в точке 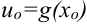 . Тогда сложная функция
. Тогда сложная функция 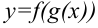 непрерывна в точке
непрерывна в точке  .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Замечательные пределы. |
| Непрерывность функции в точке и на промежутке. |
| Свойства функций, непрерывных на отрезке. |
| Непрерывность элементарных и сложных функций. |
