Пусть функция 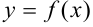 определена в точке
определена в точке  и некоторой окрестности этой точки.
и некоторой окрестности этой точки.
Функция 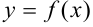 называется непрерывной в точке
называется непрерывной в точке  , если существует предел функции в этой точке и он равен значению функции в этой точке, т.е.
, если существует предел функции в этой точке и он равен значению функции в этой точке, т.е.
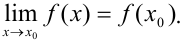
Пример №10.1.
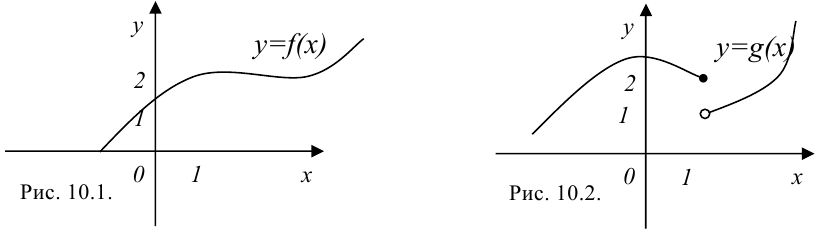
На основании определения непрерывной функции выясните, являются ли функции 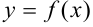 и
и 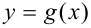 на рис. 10.1 и 10.2 непрерывными в точке
на рис. 10.1 и 10.2 непрерывными в точке 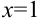 .
.
Решение:
Функции 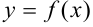 и
и 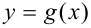 определены в точке
определены в точке 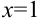 и некоторой окрестности этой точки. Найдем предел и значение функций в данной точке.
и некоторой окрестности этой точки. Найдем предел и значение функций в данной точке.
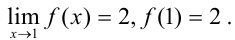 Видим, что
Видим, что 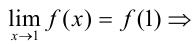 функция
функция 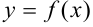 непрерывна в точке
непрерывна в точке 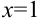 .
.
Для функции 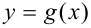 , хотя функция определена в точке
, хотя функция определена в точке 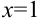 ,
, 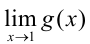 не существует. Следовательно, функция
не существует. Следовательно, функция 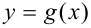 не является непрерывной в точке
не является непрерывной в точке 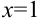 .
.
Функция 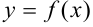 называется непрерывной на промежутке (
называется непрерывной на промежутке (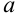 ;
; 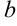 ). если она непрерывна в каждой точке этого промежутка.
). если она непрерывна в каждой точке этого промежутка.
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Предел функции на бесконечности. |
| Замечательные пределы. |
| Основные теоремы о непрерывных функциях. |
| Свойства функций, непрерывных на отрезке. |

