Оглавление:
Рассмотрим правило нахождения предела функции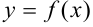 
в точке 
.
4.1. Если под знаком предела стоит многочлен, то предел вычисляется простой подстановкой (приём замены аргумента его предельным значением).
Пример №9.3.
Вычислите: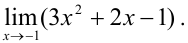 
Решение:
Подставим в многочлен вместо 
значение -1, тогда
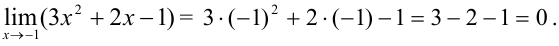
4.2. Если под знаком предела стоит отношение двух многочленов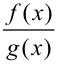 
, то проверяем, обращается ли при подстановке знаменатель в ноль. Если не обращается, то предел вычисляется простой подстановкой (см. пример 9.2).
Если при подстановке знаменатель обращается в ноль, то необходимо использовать дополнительные приемы.
Если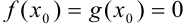 
, то имеем неопределенность вида 
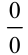. В этом случае предел 
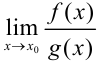можно вычислить разложением многочленов 
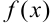и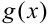 
на множители, используя формулы сокращенного умножения и формулу разложения квадратного трехчлена на множители:
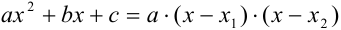, где 
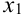и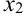 
— корни уравнения 
.
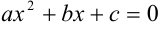Если разложение выполнено верно, то в числителе и знаменателе дроби должны получиться одинаковые множители, которые следует сократить. После сокращения предел вычисляется простой подстановкой.
Пример №9.4.
Вычислите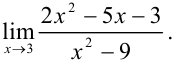 
Решение:
Проверим, какие значения будут принимать числитель и знаменатель при подстановке вместо значения 3: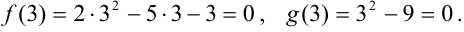 
Получили неопределенность вида .
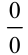Разложим числитель на множители по формуле разложения квадратного трехчлена. Составим уравнение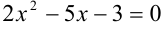 
и найдем его корни:
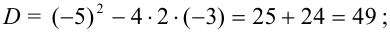
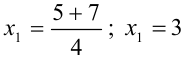или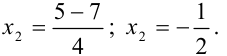 
Тогда числитель можно представить в виде произведения двух множителей:
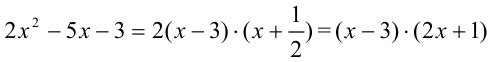
Знаменатель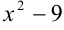 
разложим по формуле разности квадратов: 
.
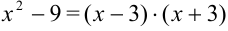Вернемся к исходному пределу:
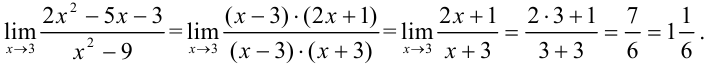
Ответ: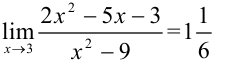 
4.3. Если под знаком предела стоит дробь вида 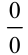, включающая иррациональную функцию (функцию, содержащую корень), то домножаем числитель и знаменатель дроби на выражение, сопряженное иррациональному.
Пример №9.5.
Вычислите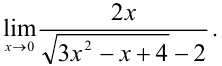 
Решение:
Поскольку при подстановке в числитель и знаменатель вместо значение 0, получаем неопределенность 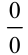, домножим числитель и знаменатель дроби на выражение 
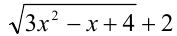, сопряженное знаменателю. Получим:
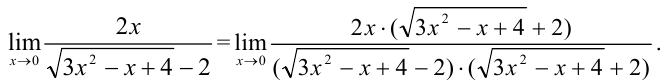
В знаменателе дроби воспользуемся формулой разности квадратов:
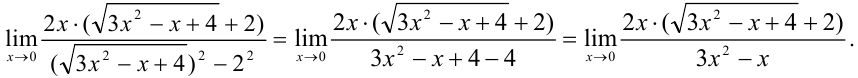
Вынесем в знаменателе за скобки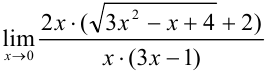 
и сократим дробь на : 
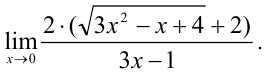
Видим, что при подстановке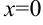 
числитель и знаменатель не обращаются в 0, следовательно, теперь предел вычисляется простой подстановкой:
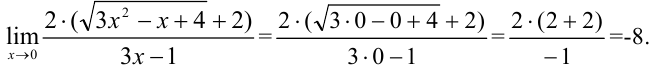
Ответ: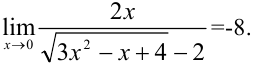 
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Односторонние пределы. |
| Основные теоремы о пределах функции. |
| Предел функции на бесконечности. |
| Замечательные пределы. |
