Не всякая последовательность имеет предел. Сформулируем признак существования предела последовательности.
Теорема Вейерштрасса. Всякая монотонная ограниченная последовательность имеет предел.
В качестве примера рассмотрим последовательность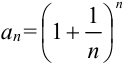 
. Выпишем элементы этой последовательности:
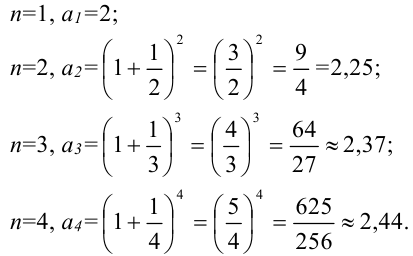
Видим, что каждый следующий элемент последовательности больше предыдущего. Данная последовательность является возрастающей.
Кроме того, данная последовательность ограничена, при этом для любого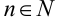 
справедливо неравенство: 
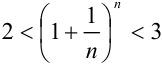. Следовательно, на основании теоремы Вейерштрасса последовательность 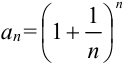имеет предел, равный 
: 
.
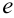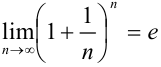Существование этого предела впервые установил Д.Бернулли в 1728 году.
Число 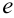— иррациональное число, его приближенное значение равно 2,72 ( 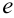= 2,718281828459045…). Число 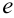называют неперовым числом, а обозначение 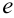введено Эйлером в начале XVIII века.
Отметим, что число 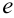является основанием логарифма, получившего название натурального: 
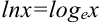. Натуральные логарифмы наиболее часто употребляются на практике.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Предел последовательности. Свойства предела. |
| Бесконечно малые и бесконечно большие последовательности. |
| Понятие предела функции. |
| Односторонние пределы. |
