Числовая последовательность называется бесконечно малой, если ее предел равен нулю.
Например, последовательность 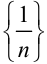 является бесконечно малой, так как ее предел равен нулю (
является бесконечно малой, так как ее предел равен нулю (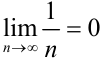 ). Последовательность
). Последовательность 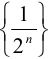 также бесконечно малая, так как
также бесконечно малая, так как 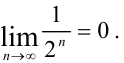
Последовательность {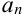 } называется бесконечно большой, если для любого наперед заданного положительного числа
} называется бесконечно большой, если для любого наперед заданного положительного числа 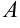 найдется такой номер элемента
найдется такой номер элемента 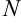 , что для всех
, что для всех 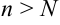 выполняется неравенство
выполняется неравенство 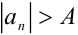 . В этом случае пишут:
. В этом случае пишут: 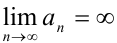 .
.
Пример №8.5.
Покажите, что числовая последовательность {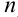 } — бесконечно большая.
} — бесконечно большая.
Решение:
Какое бы положительное число 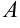 мы ни выбрали (например,
мы ни выбрали (например, 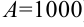 ), найдется равное ему (если
), найдется равное ему (если 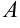 — натуральное) или большее его натуральное число
— натуральное) или большее его натуральное число 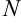 (
(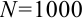 ), что для всех
), что для всех 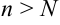 (
(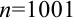 ) выполняется неравенство
) выполняется неравенство 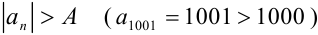 . Следовательно,
. Следовательно, 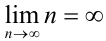 , т.е. числовая последовательность {
, т.е. числовая последовательность {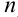 }- бесконечно большая.
}- бесконечно большая.
Аналогично, числовая последовательность 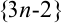 из примера 8.2 — бесконечно большая и
из примера 8.2 — бесконечно большая и 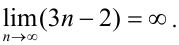
Установим связь между бесконечно большими и бесконечно малыми последовательностями.
Теорема. Пусть {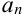 } — бесконечно большая последовательность, тогда последовательность обратных величин
} — бесконечно большая последовательность, тогда последовательность обратных величин 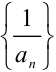 — бесконечно малая.
— бесконечно малая.
И обратно, если {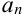 } — бесконечно малая последовательность (причем
} — бесконечно малая последовательность (причем 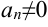 ), тогда последовательность обратных величин
), тогда последовательность обратных величин 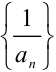 — бесконечно большая.
— бесконечно большая.
Так, если последовательность {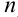 } — бесконечно большая, то последовательность обратных величин
} — бесконечно большая, то последовательность обратных величин 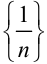 — бесконечно малая.
— бесконечно малая.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Ограниченные и неограниченные последовательности. |
| Предел последовательности. Свойства предела. |
| Признак сходимости монотонной последовательности. Число e. |
| Понятие предела функции. |

