Число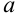 
называется пределом последовательности {
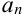}, если для любого наперед заданного положительного числа 
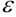найдется такое натуральное число 
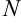, что для любого номера элемента 
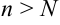выполняется неравенство: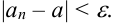 
В этом случае пишут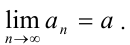 
Другими словами, какую бы точность 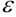мы не задали, начиная с некоторого номера 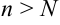все члены последовательности будут отличаться от значения предела 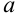на число, меньшее 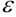, т.е. будут близки к числу .
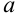Геометрически определение предела последовательности можно представить следующим образом: при достаточно больших значениях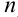 
элементы последовательности практически не отличаются от числа 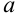(рис. 8.4). Говорят, что такие элементы попадают в 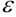-окрестность числа .
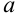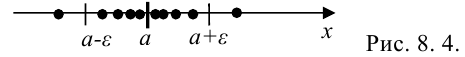
Так, в примере 8.1 с возрастанием номера 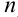элементы последовательности 
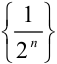все ближе и ближе приближаются к числу 0 (рис. 8.4). Покажем, что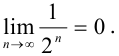 
Выберем любую точность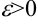 
(например, 
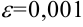). Тогда найдется натуральное число 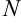(в нашем случае 
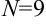), такое что для всех 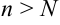выполняется неравенство: 
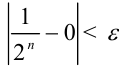(в нашем примере уже для 
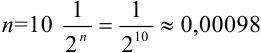будет меньше ).
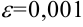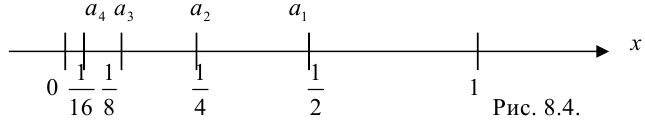
В примере 8.3 с возрастанием номера 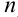элементы последовательности 
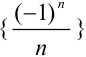приближаются к числу 0, и аналогично можно показать, что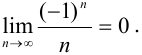 
Последовательность, имеющая предел, называется сходящейся, а не имеющая предела — расходящейся.
Так, в примере 8.2 последовательность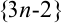 
не имеет предела, т.к. ее элементы неограниченно возрастают, следовательно, эта последовательность является расходящейся.
Последовательности, рассмотренные в примерах 8.1 и 8.3 являются сходящимися.
Еще до нашей эры философом Зеноном Эллийским (490-430 г.до н.э.) были рассмотрены задачи, содержащие в себе противоречия. Их так и называют — апории Зенона. Рассмотрим одну из таких задач, которая носит название дихотомия.
Пусть пешеходу нужно пройти из пункта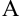 
в пункт 
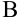. Для этого он должен сначала преодолеть половину пути, потом половину оставшегося расстояния, затем следующую половину и т.д.
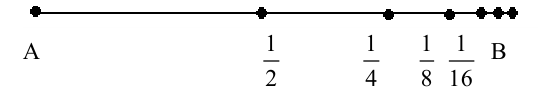
Следовательно, пешеход пройдет сначала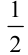 
пути, затем 
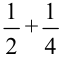пути, затем 
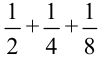пути и т.д. Какой бы маленький участок пути ни оставалось преодолеть пешеходу, очевидно, что у любого, даже самого маленького отрезка, всегда можно найти половину. И путнику вновь останется преодолеть половину этого маленького отрезка. И так до бесконечности! Парадоксально, но факт, пешеходу все время придется делить оставшийся отрезок пополам, и он никогда не придет в пункт .
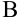Если составить алгоритм решения задачи в контексте данной логической схемы, то ни один компьютер не справится с ней — «зависнет», он будет продолжать находить середину отрезка до прерывания программы.
Посмотрим на эту задачу с точки зрения теории пределов. Расстояние, которое должен преодолеть пешеход, можно представить как сумму первых 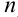элементов последовательности
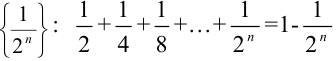. Найдем предел этой последовательности: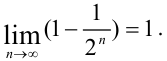 
Значит, с возрастанием 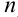длина отрезка, которую остается преодолеть пешеходу, становится ничтожно мала, и пешеход все-таки придет в пункт !
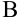Для практического нахождения пределов числовых последовательностей используют следующие свойства пределов:
Пусть {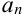} и {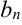
} — сходящиеся последовательности, т.е. 
, 
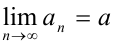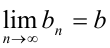. Тогда справедливы следующие утверждения:
- Всякая сходящаяся последовательность имеет только один предел.
- Для любого числа
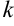последовательность {
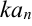} также сходится, причем 
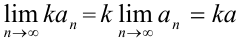. - Сумма (разность)
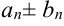также сходится, причем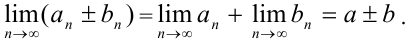 
- Произведение
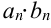также сходится, причем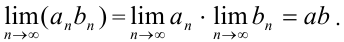 
- При дополнительном условии
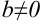частное 
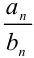также сходится, причем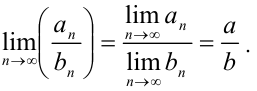 
Пример №8.4.
Найдите предел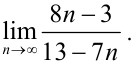 
Решение:
Числитель и знаменатель представляют собой расходящиеся последовательности (так как они не ограничены), поэтому непосредственно применять теорему о пределе частного нельзя. В этом случае поступим так: числитель и знаменатель разделим на 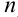(от этого дробь не изменится), а затем применим доказательные теоремы о пределах последовательностей. Приведем подробную запись вычисления предела:
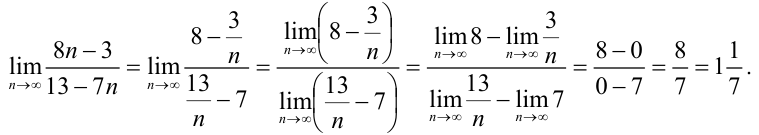
Ответ: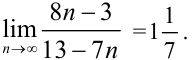 
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Монотонные последовательности. |
| Ограниченные и неограниченные последовательности. |
| Бесконечно малые и бесконечно большие последовательности. |
| Признак сходимости монотонной последовательности. Число e. |
