Оглавление:
Известные из школьного курса математики арифметическая и геометрическая прогрессии представляют собой примеры числовых последовательностей. Так, арифметическая прогрессия с первым членом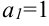 
и разностью 
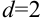есть бесконечная числовая последовательность вида: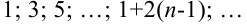 
Геометрическая прогрессия, первый член которой 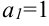и знаменатель 
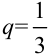, т.е. прогрессия вида 1; 
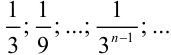— также бесконечная числовая последовательность.
Задать числовую последовательность — значит задать правило, по которому каждому натуральному числу (номеру) соответствует одно и только одно действительное число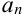 
(значение члена последовательности с номером 
).
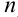Бесконечной числовой последовательностью называется функция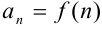 
, заданная на множестве натуральных чисел 
.
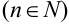Число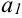 
называется первым членом последовательности, 
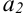— вторым, …, 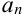— 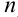-ым (общим). Индекс 1, 2, 3,…, 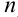— номер элемента последовательности. Для обозначения числовой последовательности принята следующая запись: {}.
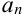Чаще всего последовательность задается с помощью формулы для нахождения 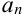, например, 
.
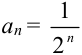Пример №8.1.
Выпишите элементы последовательности .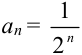
Решение:
Пусть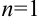 
, тогда 
.
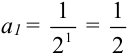Подставляя вместо 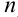значения 2, 3, 4, 5, 6 и т.д. получим остальные элементы последовательности, образующие бесконечное числовое множество:
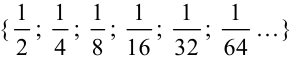
Пример №8.2.
Выпишите элементы последовательности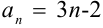 
.
Решение:
Подставляя вместо 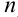значения 1, 2, 3 и т.д., найдем следующие элементы последовательности: {1; 4; 7; 10; 13; 16…}.
Пример №8.3.
Выпишите элементы последовательности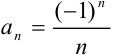 
.
Решение:
Выбирая в качестве 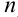значения 1, 2, 3 и т.д., получим следующие элементы последовательности: 
.
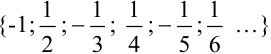Введенное понятие числовой последовательности имеет простую геометрическую интерпретацию. Отмечая на числовой оси значения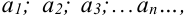 
получим множество точек, соответствующих данной последовательности.
В примере 8.1 последовательности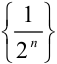 
соответствует следующее геометрическое изображение (рис. 8.1):
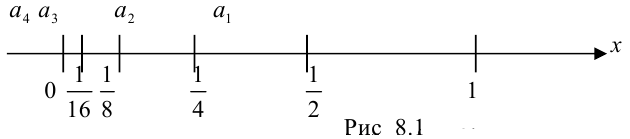
В примере 8.2 последовательности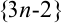 
соответствует изображение на рис. 8.2:
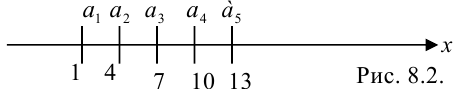
В примере 8.3 элементы последовательности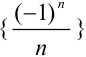 
можно представить следующим образом (рис. 8.3):
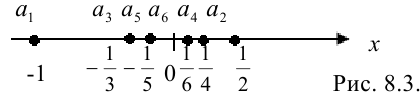
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Гипербола и ее уравнение. |
| Парабола и ее уравнение. |
| Монотонные последовательности. |
| Ограниченные и неограниченные последовательности. |
