Гиперболой называется множество точек плоскости, разность расстояний от каждой из которых до двух заданных точек (называемых фокусами) есть величина постоянная (меньшая, чем расстояние между фокусами).
Фокусы гиперболы принято обозначать буквами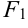 
и 
.
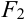Тогда по определению если точк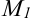и 
и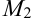 
принадлежат эллипсу, то справедливо равенство: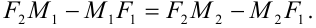 
Каноническое уравнение гиперболы имеет вид: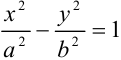 
.
Для построения гиперболы, как и эллипса, выделяем из уравнения параметры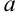 
и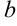 
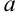( -действительная полуось, 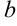— мнимая полуось).
На осях координат отмечаем точки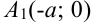 
, 
, 
, 
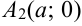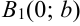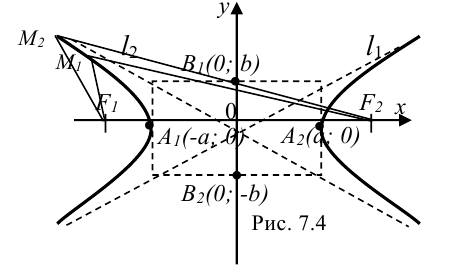
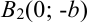. Строим прямоугольник так, как показано на рисунке 7.4.
Диагонали прямоугольника (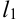
и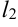 
) являются асимптотами гиперболы (ветви гиперболы «стремятся» к 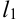и 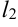, но никогда их не пересекут). Точк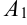и 
и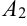 
называются вершинами гиперболы.
Пример №7.4.
Постройте гиперболу, заданную уравнением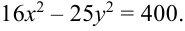 
Решение:
Приведем уравнение к каноническому виду. Для этого разделим все его члены на 400:
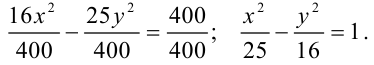
Из этого уравнения можем записать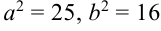 
, т.е.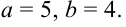 
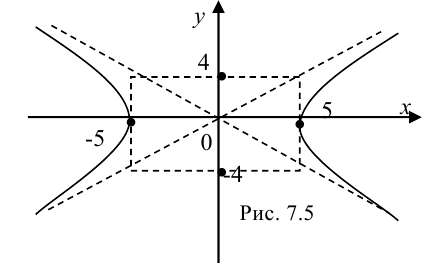
Выполним чертеж (рис. 7.5):
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Окружность и ее уравнение. |
| Эллипс и его уравнение. |
| Парабола и ее уравнение. |
| Понятие числовой последовательности. |
