Оглавление:
Окружностью называется множество точек плоскости, равноудаленных от одной точки, называемой центром.
Пусть центром окружности является точка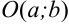 
, а расстояние до любой точки 
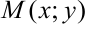окружности равно 
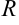(рис. 7.1). Составим уравнение окружности.
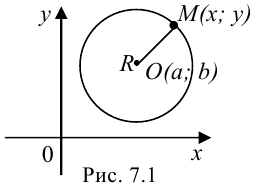
Расстояние от точки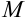 
до центра окружности можно найти, пользуясь формулой расстояния между точками:
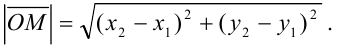
Подставив в это выражение координаты точек 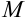и 
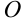, получим:
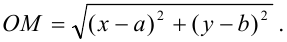
Поскольку расстояние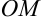 
равно радиусу 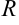, следовательно,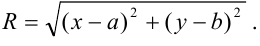 
Возведём обе части уравнения в квадрат: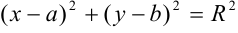 
.
Это уравнение называется каноническим уравнением окружности с центром 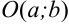и радиусом .
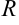Если центр окружности совпадает с началом координат, то уравнение окружности имеет вид: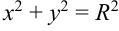 
.
Пример №7.1.
Составьте уравнение окружности с центром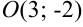 
и радиусом 
.
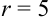Решение:
Подставив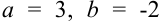 
и 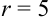в каноническое уравнение окружности 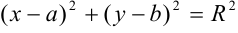, получим: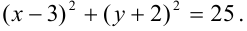 
Пример №7.2.
Докажите, что линия, заданная уравнением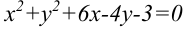 
, является окружностью, найти координаты ее центра и радиуса.
Решение:
Попытаемся привести уравнение линии к виду: 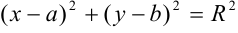. Для этого выделим в уравнении полные квадраты. Имеем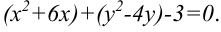 
Для получения полного квадрата к первой скобке добавим 9, ко второй 4, и вычтем числа 9 и 4 соответственно: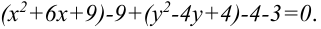 
Получим, что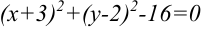 
или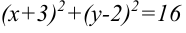 
— уравнение окружности с центром 
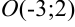и радиусом 4.
Ответ: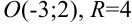 
.
