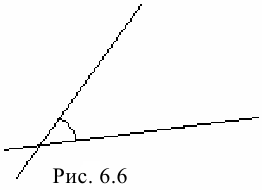
Углом между двумя прямыми называется величина меньшего из углов, образованного этими прямыми.
На рис. 6.6 углом между прямыми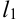 
и 
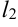является угол 
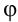. Выведем формулу для его нахождения.
Если прямая 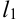задана уравнением 
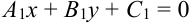, то ее нормальный вектор 
.
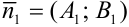Если прямая 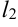задана уравнением 
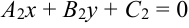, то ее нормальный вектор 
.
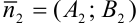Угол между векторами можно найти по формуле:
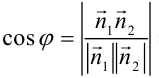, где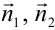 
— нормальные векторы прямых 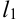и .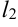
Эта формула удобна для вычисления угла между прямыми, заданными их уравнениями.
Пример №6.7.
Найдите угол между прямым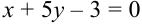и 
и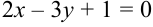 
.
Решение:
Найдем координаты нормальных векторов заданных прямых: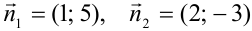 
. Согласно формуле получим
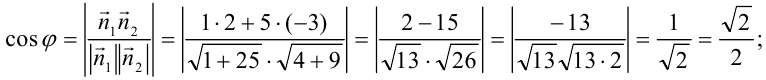
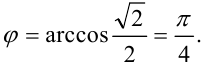Ответ: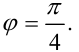 
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Способы задания прямой. |
| Виды уравнений прямой. |
| Расстояние от точки до прямой. |
| Понятие кривой второго порядка. |
