Оглавление:
Общее уравнение прямой
Справедливо следующее утверждение: всякая прямая на плоскости определяется уравнением первой степени с двумя переменными 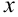 и
и 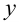 и обратно, всякое уравнение вида
и обратно, всякое уравнение вида 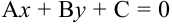 при любых действительных значениях коэффициентов
при любых действительных значениях коэффициентов 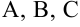 , кроме случая одновременного равенства нулю коэффициентов
, кроме случая одновременного равенства нулю коэффициентов  и
и 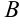 , определяет прямую.
, определяет прямую.
Уравнение 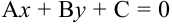 называется общим уравнением прямой. Коэффициенты
называется общим уравнением прямой. Коэффициенты 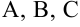 принято записывать в виде целых чисел.
принято записывать в виде целых чисел.
Уравнение прямой с угловым коэффициентом k
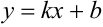 — уравнение прямой с угловым коэффициентом
— уравнение прямой с угловым коэффициентом 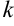 .
.
3.3. Каноническое уравнение прямой. Уравнение вида 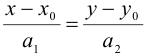 , где
, где 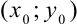 — координаты точки, принадлежащей прямой,
— координаты точки, принадлежащей прямой, 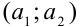 — координаты направляющего вектора, называется каноническим уравнением прямой.
— координаты направляющего вектора, называется каноническим уравнением прямой.
Параметрическое уравнение прямой.
Обозначим буквой 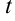 каждое из равных отношений канонического уравнения прямой. Получим, что
каждое из равных отношений канонического уравнения прямой. Получим, что
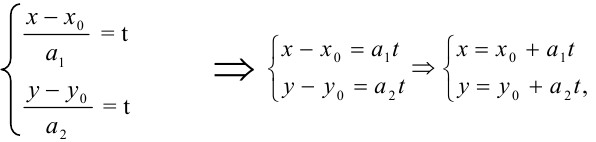
где 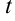 — параметр, который может принимать любые числовые значения. Такую систему уравнений называют параметрическим уравнением прямой.
— параметр, который может принимать любые числовые значения. Такую систему уравнений называют параметрическим уравнением прямой.
Пример №6.6.
Запишите уравнение прямой 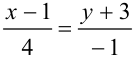
- в параметрическом виде;
- в общем виде;
- с угловым коэффициентом;
- построить данную прямую.
Решение:
1. Если задано каноническое уравнение прямой, то из формулы 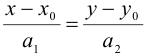 можно выделить координаты направляющего вектора (4; -1) и точки, лежащей на прямой (1; -3). Пользуясь этими данными, составим параметрическое уравнение прямой:
можно выделить координаты направляющего вектора (4; -1) и точки, лежащей на прямой (1; -3). Пользуясь этими данными, составим параметрическое уравнение прямой:
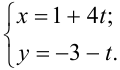
2. Для составления общего уравнения прямой, воспользуемся свойством пропорции:
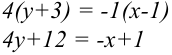
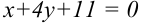 — общее уравнение прямой.
— общее уравнение прямой.
3. Для составления уравнения данной прямой с угловым коэффициентом, из общего уравнения прямой выразим 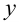 :
:
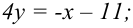
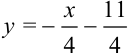 — уравнение прямой с угловым коэффициентом
— уравнение прямой с угловым коэффициентом 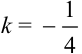 .
.
4. Строить прямую удобнее всего, пользуясь её параметрическим заданием. Пусть 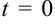
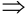 точка (1; -3) принадлежит прямой;
точка (1; -3) принадлежит прямой;
Пусть 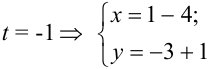 . Точка (-3;-2) также лежит на прямой.
. Точка (-3;-2) также лежит на прямой.
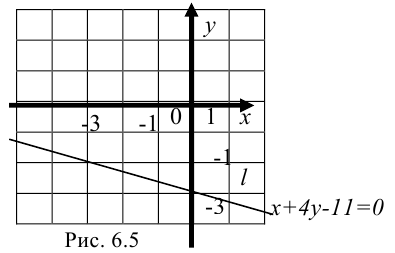
Построим прямую, проходящую через две полученные точки (рис.6.5):
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Уравнение линии на плоскости. |
| Способы задания прямой. |
| Угол между двумя прямыми. |
| Расстояние от точки до прямой. |

