Оглавление:
Все возможные операции, которые можно выполнять над векторами в координатах, представим в виде таблицы 5.1:
Таблица 5.1
Операции над векторами в координатах
Справедливы следующие теоремы.
Теорема 1. Если векторы 
и 
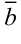коллинеарны, то их соответствующие координаты пропорциональны.
Теорема 2. Если ненулевые векторы и 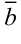взаимно перпендикулярны, то их скалярное произведение равно нулю, и наоборот, если скалярное произведение векторов равно нулю, то векторы перпендикулярны: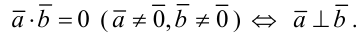
Пример №5.1.
Даны точки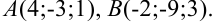 
Найдите: 1) координаты вектора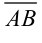 
;
2) длину вектора ;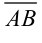
3) координаты точки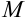 
— середины 
.
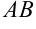Решение:
1) Воспользуемся формулой нахождения координат вектора: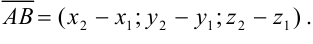 
Тогда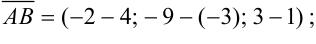 
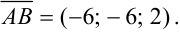
2) Зная координаты вектора 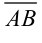, найдем его длину по формуле: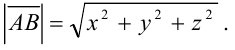 
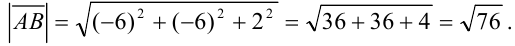
3) Пусть точка 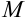— середина отрезка 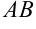. Тогда ее координаты находятся по формуле: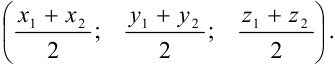 
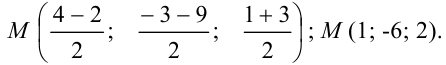
Ответ: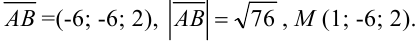 
Пример №5.2.
Даны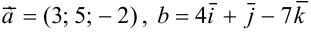 
.
Найдите:
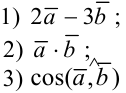
Решение:
1) Вектор 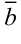задан в виде разложения по базисным векторам 
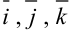. Его координаты находятся как коэффициенты разложения вектора по базису: 
.
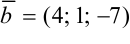Найдем координаты векторов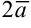 
и 
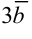по формуле: 
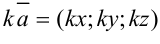. Тогда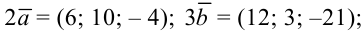 
Воспользуемся формулой нахождения суммы и разности векторов:
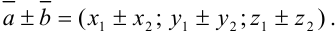Получим, что
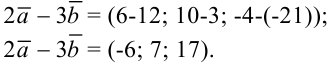
2) Воспользуемся формулой нахождения скалярного произведения векторов:
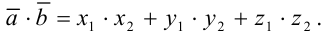
Получим:
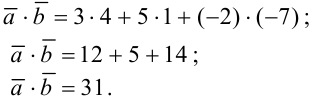
3) Найдем косинус угла между векторами по формуле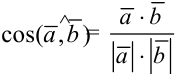 
.
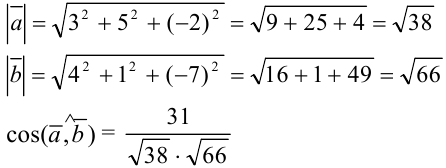
Ответ:
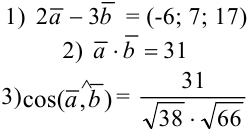
Пример №5.3.
При каком значении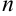 
векторы 
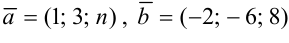1) коллинеарны; 2) перпендикулярны?
Решение:
1) Воспользуемся теоремой 1: если векторы коллинеарны, то их соответствующие координаты пропорциональны. Получим, что
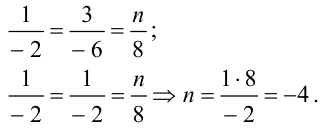
Следовательно, при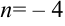 
векторы и 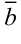коллинеарны.
2) Воспользуемся теоремой 2: если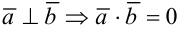 
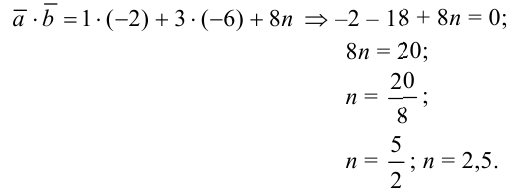
Следовательно, при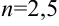 
векторы и 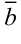перпендикулярны.
Ответ: 1) 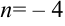; 2) .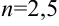
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Скалярное произведение векторов. |
| Координаты вектора на плоскости и в пространстве. |
| Уравнение линии на плоскости. |
| Способы задания прямой. |
