Оглавление:
Теорема. Определитель равен сумме произведений элементов любой строки или столбца определителя на их алгебраические дополнения:
Рассмотрим разложение определителя по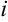 
-й строке:
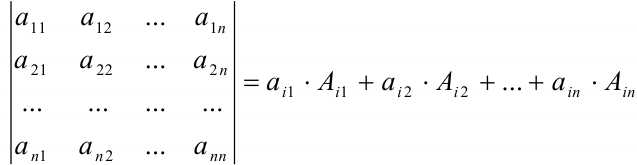
Разложение определителя по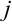 
-му столбцу:
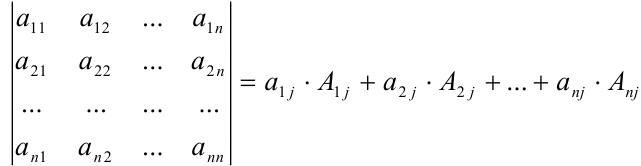
Данная теорема позволяет вычислять определитель по любой строке или по любому столбцу. Важно помнить, что, вычисляя определитель разными способами, ответ должен быть одним и тем же. В качестве ряда, по которому будет раскрываться определитель, целесообразно выбирать ряд, содержащий большее количество нулей.
Пример №2.8.
Вычислите определитель: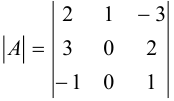 
а) по первой строке;
б) по второму столбцу.
Решение:
Раскроем определитель по первой строке:
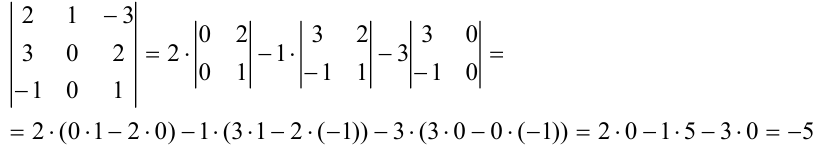
Разложим определитель по второму столбцу:
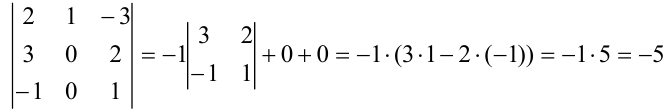
При разложении определителя по первой строке и второму столбцу получили одинаковые значения: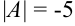 
.
Ответ: .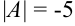
Теорема о разложении определителя по элементам строки или столбца позволяет вычислять определители более высоких порядков (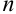
) сведением их к определителям более низких порядков 
.
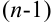Пример №2.9.
Вычислите определитель четвертого порядка
Решение:
Раскроем определить по первой строке:
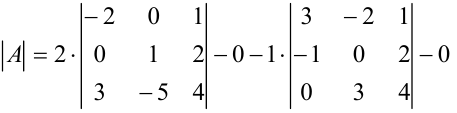
Вычислим каждый из определителей третьего порядка отдельно:
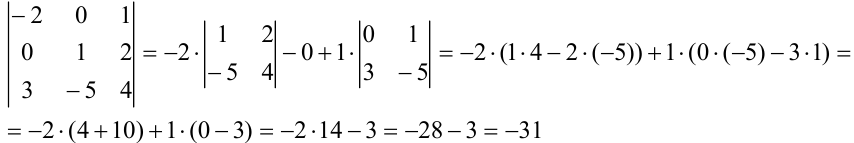
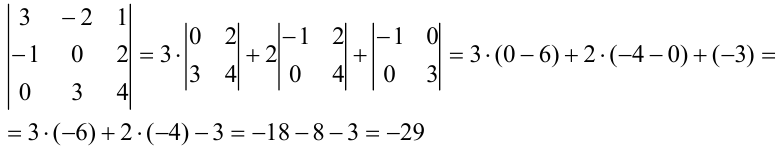
Получим, что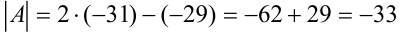 
Ответ: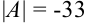 
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Свойства определителей. |
| Миноры и алгебраические дополнения элементов определителя. |
| Расчет определителей в электронных таблицах Microsoft Excel. |
| Понятие обратной матрицы. |
