Оглавление:



Зависимость теплоемкости от температуры
- Эксперименты показали, что при повышении температуры газа вибрационное движение атомов в молекуле усиливается, и требуется больше энергии. Поэтому, чем выше температура, тем больше тепла придется потратить на нагрев газа на G. следовательно, теплоемкость газа Рис. 3.2 . Функция температуры, а не константа value. In в общем случае удельная теплоемкость температуры/может быть выражена следующим уравнением с =c₀₀h-а! B-BH-LR B- (3.19). Где находится удельная теплоемкость при 0°C?
Поскольку влияние на величину термина температуры выше первой температуры очень мало, то в технических расчетах часто берут линейную зависимость теплоемкости от температуры и выражают ее формулой С -=c₀ х-а/. (3.20 утра)) На рисунке 3.2 показан график зависимости теплоемкости от температуры. Кривая строится по формуле (3.19), а прямая-по формуле (3.20).
Если с течением времени изменяется температура окружающей среды или коэффициент теплообмена а. Людмила Фирмаль
В дальнейшем будем использовать только формулу (3.20), то есть линейную зависимость теплоемкости от температуры. Из-за того, что теплоемкость зависит от температуры, расход тепла в случае одного и того же повышения температуры будет меняться. Чем выше начальная температура нагрева, тем больше тепла должно быть потреблено для того же повышения температуры. Это хорошо видно на рисунке.
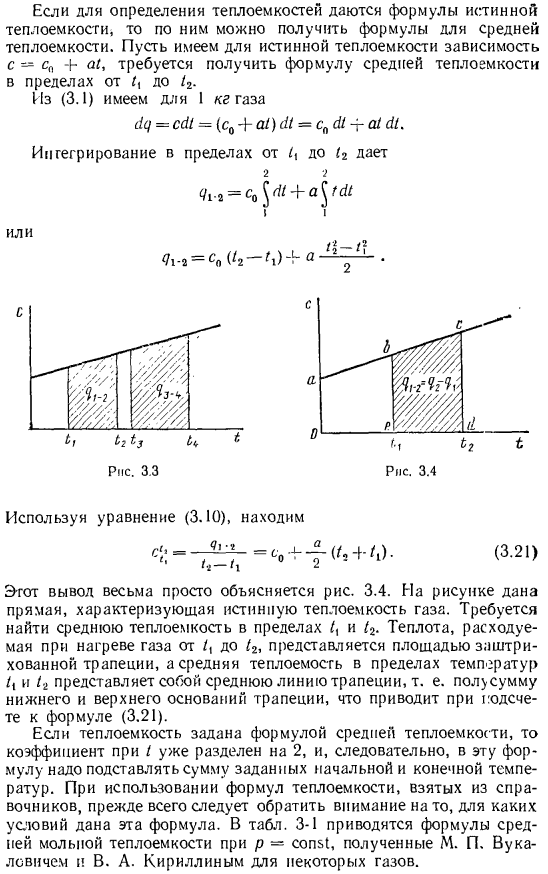
- Трапециевидная заштрихованная область представляет собой расход тепла между нагреванием газа до / ОТ / и 1g-I равен~ / равному. Если дана истинная формула теплоемкости для определения удельной теплоемкости, то из них можно получить формулу для средней удельной теплоемкости. Для истинной теплоемкости предположим, что нужно получить формулу для средней теплоемкости в диапазоне от I до 1 г, так как существует зависимость c-c» 4-a1″. (3.1) до 1 кг газа =сЛ=(с₀+о/)А=с₀4-а/ л Интеграция с меня, чтобы дать Или Рисунок 3.3 рисунок 3.4 (3.21) Используя формулу(3.10)、 Этот вывод объясняется довольно просто цифрой.
Приведена диаграмма Прямая линия, характеризующая истинную теплоемкость газа. Необходимо найти среднюю теплоемкость в I, и/₂. Теплота, потребляемая при нагревании газа от/до/, представлена площадью штрихованной трапеции, а средняя теплоемкость в диапазоне температур 1 г представляет собой сумму трапециевидной средней линии, то есть дна трапеции и половины верхнего дна, и уравнения (3.21). Если удельная теплоемкость задается формулой средней удельной теплоемкости, то коэффициент I уже делится на 2, поэтому в эту формулу необходимо подставить сумму заданных начальных и конечных температур.
Однако чаще известны лишь температура жидкости, омывающей стенку, и коэффициент теплообмена на ее поверхности. Людмила Фирмаль
При использовании формулы теплоемкости, полученной из эталона, в первую очередь необходимо обратить внимание на условия, при которых эта формула находится given. In стол. 3-1, приведена формула для средней молярной теплоемкости при р = const (для некоторых газов это М. П. Вука-ловец и В. А. Кирилин. 28、97 + 0.002566 / 28.78 + 0.001117 / 29.56 + 0.003404 / 29.06 + 0.002818 / 28.09 + 0.002412 / 32.85+ 0.00544 / 36.05 + 0.0203 / + 0.00000642 / * В таблице приведены последние экспериментальные данные по теплоемкости, полученные спектроскопически. Потому что обработка этих данных в виде выражения дает очень сложный результат.
Расчет теплопотребления с учетом этих данных выглядит следующим образом (рис. 3.4): Если вы знаете только среднюю теплоемкость в диапазоне от 0 до GS, вам нужно найти потребление тепла для нагрева газа от I до ( ₂ ).Поэтому вам нужно найти площадь трапеции LcMr. Эта область представляет собой тепло, затрачиваемое на нагрев газа от 0°до 0°, и тепло, затрачиваемое на нагрев того же газа от 0 ° до/ / C. Таким образом, площадь трапеции ba1eB определяет тепло. от₍к。. Так… Яг-я — н-8-OassU-ЛП. Да. Но… пл. С/гсйО=/?,=с ’,’ / ₄ ; пл. OaBeO = ХХ = с ‘*. Тепло, необходимое для нагрева газа от I до ₂ 7. ; = с ’-/» .- «’ ■ / !•(3.22) В этом выражении/, и / 2 Тепло capacity.
Смотрите также:
| Характеристики политропных процессов в зависимости от значения показателя n | Теплоемкость газовой смеси |
| Теплоемкость идеального газа | Отношение теплоемкостей |

