Оглавление:
Функциональные ряды
Основные понятия
Ряд, членами которого являются функции от  , называется функциональным:
, называется функциональным:
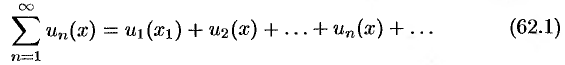
Придавая  определенное значение
определенное значение  , мы получим числовой ряд
, мы получим числовой ряд
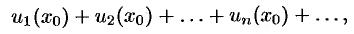
который может быть как сходящимся, так и расходящимся.
Если полученный числовой ряд сходится, то точка  называется точкой сходимости ряда (62.1); если же ряд расходится точкой расходимости функционального ряда.
называется точкой сходимости ряда (62.1); если же ряд расходится точкой расходимости функционального ряда.
Совокупность числовых значений аргумента  , при которых функциональный ряд сходится, называется его областью сходимости.
, при которых функциональный ряд сходится, называется его областью сходимости.
В области сходимости функционального ряда его сумма является некоторой функцией от  :
: 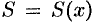 . Определяется она в области сходимости равенством
. Определяется она в области сходимости равенством
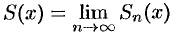 , где
, где 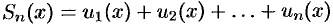 — частичная сумма ряда.
— частичная сумма ряда.
Пример №62.1.
Найти область сходимости рада 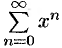 .
.
Решение:
Данный ряд является рядом геометрической прогрессии со знаменателем 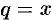 . Следовательно, этот ряд сходится при
. Следовательно, этот ряд сходится при 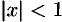 , т.е. при всех
, т.е. при всех 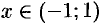 ; сумма ряда равна
; сумма ряда равна 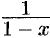 :
:
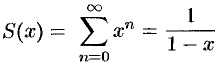 при
при 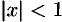 .
.
Дополнительный пример №62.2.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Функции двух переменных |
| Таблица неопределенных интегралов |
| Абсолютная и условная сходимости числовых рядов |
| Выражение векторного произведения через координаты |

