Оглавление:
Общая схема исследования функции и построения графика
Исследование функции 
целесообразно вести в определенной последовательности.
- Найти область определения функции.
- Найти (если это можно) точки пересечения графика с осями координат.
- Найти интервалы знакопостоянства функции (промежутки, на которых
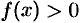или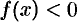 
). - Выяснить, является ли функция четной, нечетной или общего вида.
- Найти асимптоты графика функции.
- Найти интервалы монотонности функции.
- Найти экстремумы функции.
- Найти интервалы выпуклости и точки перегиба графика функции.
На основании проведенного исследования построить график функции. Заметим, что приведенная схема исследования не является обязательной. В более простых случаях достаточно выполнить лишь несколько операций, например 1, 2, 7. Если же график функции не совсем понятен и после выполнения всех восьми операций, то можно дополнительно исследовать функцию на периодичность, построить дополнительно несколько точек графика, выявить другие особенности функции. Иногда целесообразно выполнение операций исследования сопровождать постепенным построением графика функции.
Пример №25.14.
Исследовать функцию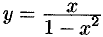 
и построить ее график.
Решение:
Выполним все восемь операций предложенной выше схемы исследования.
1. Функция не определена пр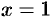и 
и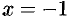 
. Область ее определения состоит из трех интервалов 
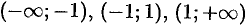, а график из трех ветвей.
2. Если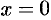 
, то 
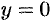. График пересекает ось 
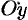в точке 
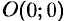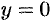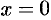; если , то . График пересекает ось 
в точке .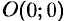
3. Функция знакоположительна (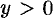
) в интервалах 
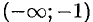и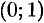 
; знакоотрицательна — в 
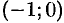и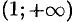 
.
4. Функция 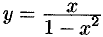является нечетной, т. к.
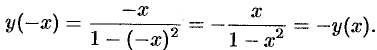
Следовательно, график ее симметричен относительно начала координат. Для построения графика достаточно исследовать ее при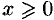 
.
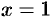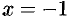5. Прямые и являются ее вертикальными асимптотами. Выясним наличие наклонной асимптоты:
(
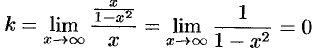
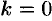при 
и при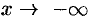 
),
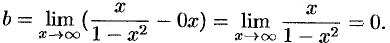
Следовательно, есть горизонтальная асимптота, ее уравнение .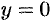
Прямая 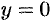является асимптотой и при , и при .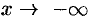
6. Находим интервалы возрастания и убывания функции. Так как
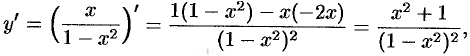
то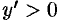 
в области определения, и функция является возрастающей на каждом интервале области определения.
7. Исследуем функцию на экстремум. Так как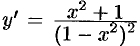 
, то критическими точками являются точк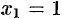и 
и 
(
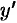не существует), но они не принадлежат области определения функции. Функция экстремумов не имеет.
8. Исследуем функцию на выпуклость. Находим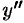 
:
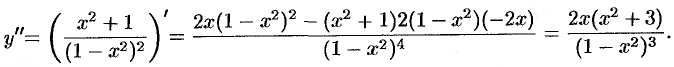
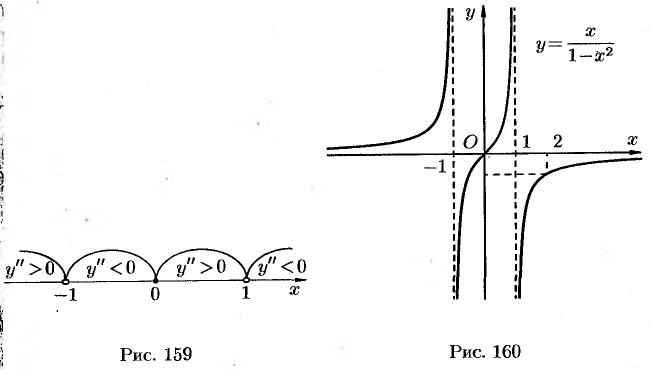
Вторая производная равна нулю или не существует в точках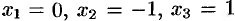 
. На рисунке 159 представлена схема изменения Знаков второй производной исследуемой функции.
Точка 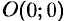— точка перегиба графика функции.
График выпуклый вверх на интервалах 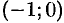и 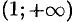; выпуклый вниз на интервалах 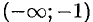и .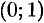
График функции изображен на рисунке 160.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Выпуклость графика функции. Точки перегиба |
| Асимптоты графика функции |
| Функции двух переменных |
| Таблица неопределенных интегралов |
