Оглавление:
Выпуклость графика функции. Точки перегиба
График дифференцируемой функции  называется выпуклым вниз на интервале
называется выпуклым вниз на интервале  , если он расположен выше любой ее касательной на этом интервале. График функции
, если он расположен выше любой ее касательной на этом интервале. График функции  называется выпуклым вверх на интервале
называется выпуклым вверх на интервале  , если он расположен ниже любой ее касательной на этом интервале.
, если он расположен ниже любой ее касательной на этом интервале.
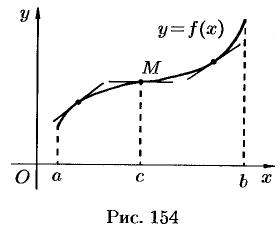
Точка графика непрерывной функции  , отделяющая его части разной выпуклости, называется точкой перегиба.
, отделяющая его части разной выпуклости, называется точкой перегиба.
На рисунке 154 кривая  выпукла вверх в интервале
выпукла вверх в интервале 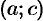 , выпукла вниз в интервале
, выпукла вниз в интервале 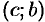 , точка
, точка 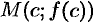 — точка перегиба.
— точка перегиба.
Интервалы выпуклости вниз и вверх находят с помощью следующей теоремы.
Теорема 25.11. Если функция  во всех точках интервала
во всех точках интервала  имеет отрицательную вторую производную, т. е.
имеет отрицательную вторую производную, т. е. 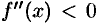 , то график функции в этом интервале выпуклый вверх. Если же
, то график функции в этом интервале выпуклый вверх. Если же 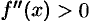
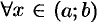 — график выпуклый вниз.
— график выпуклый вниз.
Пусть 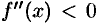
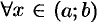 . Возьмем на графике функции произвольную точку
. Возьмем на графике функции произвольную точку  с абсциссой
с абсциссой 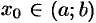 и проведем через
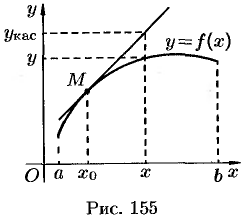
и проведем через  касательную (см. рис. 155). Покажем, что график функции расположен ниже этой касательной. Для этого сравним в точке
касательную (см. рис. 155). Покажем, что график функции расположен ниже этой касательной. Для этого сравним в точке 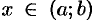 ординату у кривой
ординату у кривой  с ординатой
с ординатой 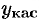 ее касательной. Уравнение касательной, как известно, есть
ее касательной. Уравнение касательной, как известно, есть
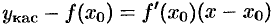 , т. е.
, т. е. 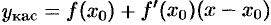 . Тогда
. Тогда 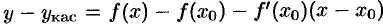 . По теореме Лагранжа,
. По теореме Лагранжа, 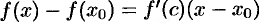 , где
, где 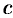 лежит между
лежит между  и
и  . Поэтому
. Поэтому
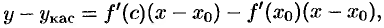
т. е.
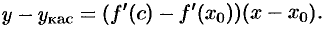
Разность 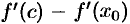 снова преобразуем по формуле Лагранжа:
снова преобразуем по формуле Лагранжа:
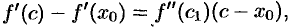
где 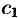 лежит между
лежит между  и
и 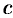 . Таким образом, получаем
. Таким образом, получаем
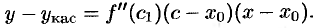
Исследуем это равенство:
1) если  , то
, то 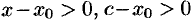 и
и 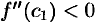 . Следовательно,
. Следовательно, 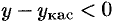 , т. е.
, т. е. 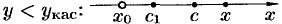
2) если 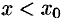 , то
, то 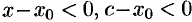 и
и 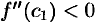 . Следовательно,
. Следовательно, 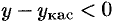 , т. е.
, т. е. 
Итак, доказано, что во всех точках интервала  ордината касательной больше ординаты графика, т. е. график функции выпуклый вверх. Аналогично доказывается, что при
ордината касательной больше ординаты графика, т. е. график функции выпуклый вверх. Аналогично доказывается, что при 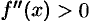 график выпуклый вниз.
график выпуклый вниз.
Для нахождения точек перегиба графика функции используется следующая теорема.
Теорема 25.12 (достаточное условие существования точек перегиба). Если вторая производная 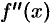 при переходе через точку
при переходе через точку  , в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой
, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой  есть точка перегиба.
есть точка перегиба.
Пусть 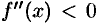 при
при 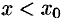 и
и 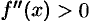 при
при  . Это значит, что слева от
. Это значит, что слева от 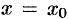 график выпуклый вверх, а справа — выпуклый вниз. Следовательно, точка
график выпуклый вверх, а справа — выпуклый вниз. Следовательно, точка 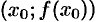 графика функции является точкой перегиба.
графика функции является точкой перегиба.
Аналогично доказывается, что если 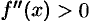 при
при 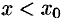 и
и 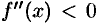 при
при  , то точка
, то точка 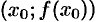 — точка перегиба графика функции
— точка перегиба графика функции  .
.
Пример №25.12.
Исследовать на выпуклость и точки перегиба график функции 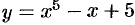 .
.
Решение:
Находим, что 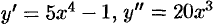 . Вторая производная существует на всей числовой оси;
. Вторая производная существует на всей числовой оси; 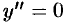 при
при 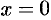 .
.
Отмечаем, что 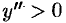 при
при 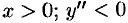 при
при 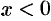 .
.
Следовательно, график функции 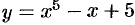 в интервале
в интервале 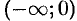 — выпуклый вверх, в интервале
— выпуклый вверх, в интервале 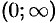 — выпуклый вниз. Точка (0; 5) есть точка перегиба.
— выпуклый вниз. Точка (0; 5) есть точка перегиба.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Максимум и минимум функций |
| Наибольшее и наименьшее значения функции на отрезке |
| Асимптоты графика функции |
| Общая схема исследования функции и построения графика |

