Оглавление:
Наибольшее и наименьшее значения функции на отрезке
Пусть функция  непрерывна на отрезке
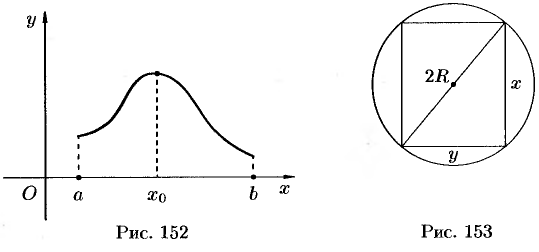
непрерывна на отрезке  . Как известно, такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке
. Как известно, такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке  отрезка
отрезка  , либо на границе отрезка, т. е. при
, либо на границе отрезка, т. е. при 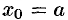 или
или 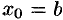 . Если
. Если 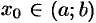 , то точку
, то точку  следует искать среди критических точек данной функции (см. рис. 152).
следует искать среди критических точек данной функции (см. рис. 152).
Получаем следующее правило нахождения наибольшего и наименьшего значений функции на  :
:
1) найти критические точки функции на интервале  ;
;
2) вычислить значения функции в найденных критических точках;
3) вычислить значения функции на концах отрезка, т. е. в точках 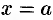 и
и 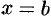 ;
;
4) среди всех вычисленных значений функции выбрать наибольшее и наименьшее.
Замечания: 1. Если функция  на отрезке
на отрезке  имеет лишь одну критическую точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение. На рисунке 152
имеет лишь одну критическую точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение. На рисунке 152 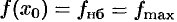 (
(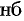 — наибольшее,
— наибольшее, 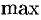 — максимальное).
— максимальное).
2. Если функция  на отрезке
на отрезке  не имеет критических точек, то это означает, что на нем функция монотонно возрастает или убывает. Следовательно, свое наибольшее значение (
не имеет критических точек, то это означает, что на нем функция монотонно возрастает или убывает. Следовательно, свое наибольшее значение ( ) функция принимает на одном конце отрезка, а наименьшее (
) функция принимает на одном конце отрезка, а наименьшее ( ) — на другом.
) — на другом.
Пример №25.10.
Найти наибольшее и наименьшее значения функции 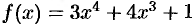 на отрезке [-2; 1].
на отрезке [-2; 1].
Решение:
Находим критические точки данной функции:
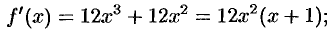
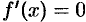 при
при 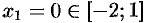 и при
и при 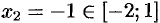 . Находим
. Находим 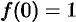 ,
, 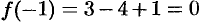 ,
,  ,
, 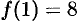 . Итак,
. Итак, 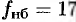 в точке
в точке 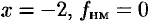 в точке
в точке 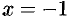 .
.
Нахождение наибольшего и наименьшего значений функции широко применяется при решении многих практических задач математики физики, химии, экономики и других дисциплин.
Практические задачи: транспортная задача о перевозке груза с минимальными затратами, задача об организации производственного процесса с целью получения максимальной прибыли и другие задачи, связанные с поиском оптимального решения, приводят к развитию и усовершенствованию методов отыскания наибольших и наименьших значений. Решением таких задач занимается особая ветвь математики — линейное программирование.
Рассмотрим более простую задачу в примере №25.11.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Возрастание и убывание функций |
| Максимум и минимум функций |
| Выпуклость графика функции. Точки перегиба |
| Асимптоты графика функции |

