Оглавление:
Максимум и минимум функций
Точка 
называется точкой максимума функции 
, если существует такая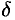 
-окрестность точки , что для всех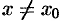 
из этой окрестности выполняется неравенство 
.
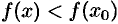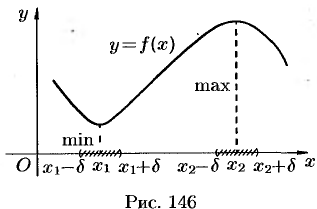
Аналогично определяется точка минимума функции: — точка минимума функции, если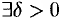 
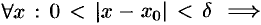
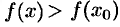. На рисунке 146 
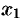— точка минимума, а точка 
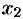— точка максимума функции .
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум (минимум) функции называется экстремумом функции.
Понятие экстремума всегда связано с определенной окрестностью точки из области определения функции. Поэтому функция может иметь экстремум лишь во внутренних точках области определения. Рассмотрим условия существования экстремума функции.
Теорема 25.8 (необходимое условие экстремума). Если дифференцируемая функция имеет экстремум в точке , то ее производная в этой точке равна нулю: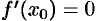 
.
Пусть, для определенности, — точка максимума. Значит, в окрестности точки выполняется неравенство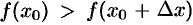 
. Но тогда 
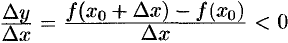, если 
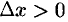, и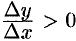 
, если 
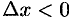. По условию теоремы производная
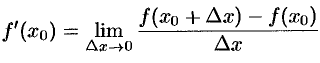
существует. Переходя к пределу, при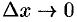 
, получим 
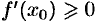, если 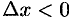, и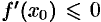 
, если 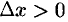. Поэтому 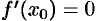. Аналогично доказывается утверждение теоремы 25.8, если — точка минимума функции 
.
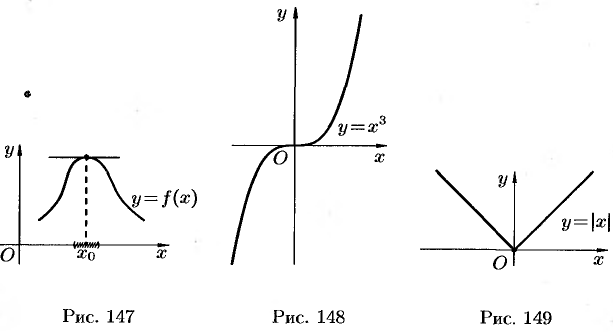
Геометрически равенство 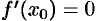означает, что в точке экстремума дифференцируемой функции касательная к ее графику параллельна оси 
(см. рис. 147).
Отметим, что обратная теорема неверна, т. е. если 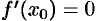, то это не значит, что — точка экстремума. Например, для функции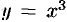 
ее производная 
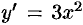равна нулю при 
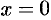, но 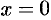не точка экстремума (см. рис. 148).
Существуют функции, которые в точках экстремума не имеют производной. Например, непрерывная функция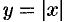 
в точке 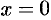производной не имеет, но точка — точка минимума (см. рис. 149).
Таким образом, непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не существует. Такие точки называются критическими.
Теорема 25.9 (достаточное условие экстремума). Если непрерывная функция дифференцируема в некоторой 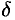-окрестности критической точки и при переходе через нее (слева направо) производная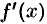 
меняет знак с плюса на минус, то есть точка максимума; с минуса на плюс, то — точка минимума.
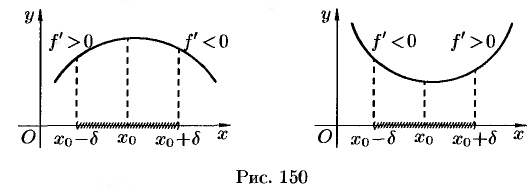
Рассмотрим 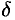-окрестность точки . Пусть выполняются условия: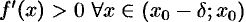 
и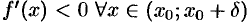 
. Тогда функция возрастает на интервале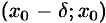 
, а на интервале 
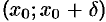она убывает. Отсюда следует, что значение в точке является наибольшим на интервале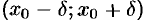 
, т. е. 
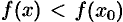для всех 
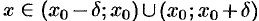. Это и означает, что — точка максимума функции.
Графическая интерпретация доказательства теоремы 25.9 представлена на рисунке 150.
Аналогично теорема 25.9 доказывается для случая, когда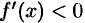 
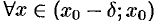и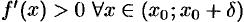 
.
Исследовать функцию на экстремум означает найти все ее экстремумы. Из теорем 25.8 и 25.9 вытекает следующее правило исследования функции на экстремум:
1) найти критические точки функции ;
2) выбрать из них лишь те, которые являются внутренними точками области определения функции;
3) исследовать знак производной 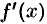слева и справа от каждой из выбранных критических точек;
4) в соответствии с теоремой 25.9 (достаточное условие экстремума) выписать точки экстремума (если они есть) и вычислить значения функции в них.
Пример №25.9.
Найти экстремум функции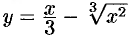 
.
Решение:
Очевидно,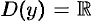 
. Находим 
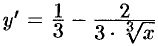, т.е. 
.
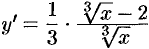Производная не существует при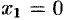 
и равна нулю при 
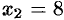. Эти точки разбивают всю область определения данной функции на три интервала 
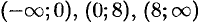. Отметим на рисунке 151 знаки производной слева и справа от каждой из критических точек.
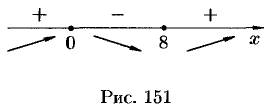
Следовательно,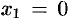 
— точка максимума, 
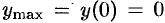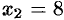, и — точка минимума, 
.
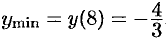Иногда бывает удобным использовать другой достаточный признак существования экстремума, основанный на определении знака второй производной.
Теорема 25.10. Если в точке первая производная функции равна нулю (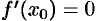), а вторая производная в точке существует и отлична от нуля (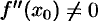
), то при 
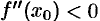в точке функция имеет максимум и минимум — при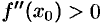 
.
Пусть для определенности 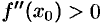. Так как
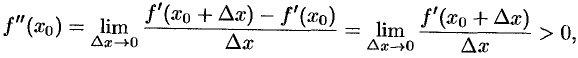
то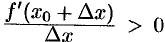 
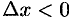в достаточно малой окрестности точки . Если , то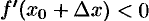 
; если 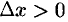, то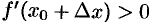 
.
Таким образом, при переходе через точку первая производная меняет знак с минуса на плюс. Следовательно, по теореме 25.9, есть точка минимума.
Аналогично доказывается, что если 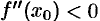, то в точке функция имеет максимум.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Теоремы о дифференцируемых функциях |
| Возрастание и убывание функций |
| Наибольшее и наименьшее значения функции на отрезке |
| Выпуклость графика функции. Точки перегиба |
