Оглавление:
Возрастание и убывание функций
Одним из приложений производной является ее применение к исследованию функций и построению графика функции.
Установим необходимые и достаточные условия возрастания и убывания функции.
Теорема 25.6 (необходимые условия). Если дифференцируемая на интервале  функция
функция  возрастает (убывает), то
возрастает (убывает), то 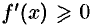
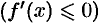 для
для 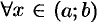 .
.
Пусть функция  возрастает на интервале
возрастает на интервале  . Возьмем произвольные точки
. Возьмем произвольные точки  и
и 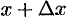 на интервале
на интервале  и рассмотрим отношение
и рассмотрим отношение 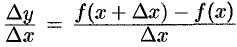 . Функция
. Функция  возрастает, поэтому если
возрастает, поэтому если 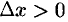 , то
, то 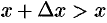 и
и 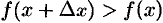 ; если
; если 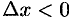 , то
, то 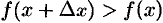 и
и 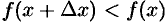 . В обоих случаях
. В обоих случаях 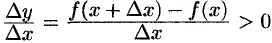 , так как числитель и знаменатель дроби имеют одинаковые знаки. По условию теоремы функция
, так как числитель и знаменатель дроби имеют одинаковые знаки. По условию теоремы функция  имеет производную в точке
имеет производную в точке  и является пределом рассматриваемого отношения. Следовательно,
и является пределом рассматриваемого отношения. Следовательно,
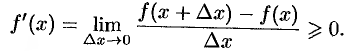
Аналогично рассматривается случай, когда функция  убывает на интервале
убывает на интервале  .
.
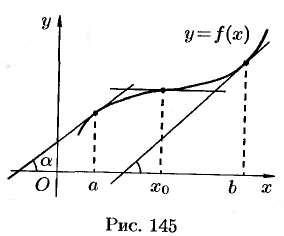
Геометрически теорема 25.6 означает, что касательные к графику возрастающей дифференцируемой функции образуют острые углы с положительным направлением оси  или в некоторых точках (на рисунке 145 в точке с абсциссой
или в некоторых точках (на рисунке 145 в точке с абсциссой  ) параллельны оси
) параллельны оси  .
.
Теорема 25.7 (достаточные условия). Если функция  дифференцируема на интервале
дифференцируема на интервале  и
и 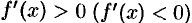 для
для 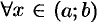 , то эта функция возрастает (убывает) на интервале
, то эта функция возрастает (убывает) на интервале  .
.
Пусть 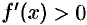 . Возьмем точки
. Возьмем точки 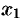 и
и 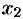 из интервала
из интервала  , причем
, причем 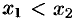 . Применим к отрезку
. Применим к отрезку 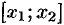 теорему Лагранжа:
теорему Лагранжа: 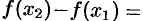
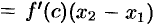 , где
, где 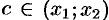 . По условию
. По условию 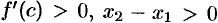 . Следовательно,
. Следовательно, 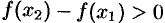 или
или 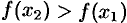 , т. е. функция
, т. е. функция  на интервале
на интервале  возрастает.
возрастает.
Рассмотренные теоремы 25.6 и 25.7 позволяют довольно просто исследовать функцию на монотонность. Напомним, что функция возрастающая или убывающая называется монотонной (см. с. 122).
Пример №25.8.
Исследовать функцию 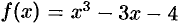 на возрастание и убывание.
на возрастание и убывание.
Решение:
Функция определена на 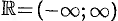 . Ее производная равна:
. Ее производная равна:
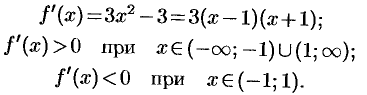
Ответ: данная функция возрастает на интервалах 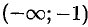 и
и 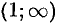 ; убывает на интервале (—1; 1).
; убывает на интервале (—1; 1).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Дифференциалы высших порядков |
| Теоремы о дифференцируемых функциях |
| Максимум и минимум функций |
| Наибольшее и наименьшее значения функции на отрезке |

