Рассмотрим ряд теорем, имеющих большое теоретическое и прикладное значение.
Теорема 25.1 (Ролль). Если функция  непрерывна на отрезке
непрерывна на отрезке  , дифференцируема на интервале
, дифференцируема на интервале  и на концах отрезка принимает одинаковые значения
и на концах отрезка принимает одинаковые значения 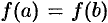 , то найдется хотя бы одна точка
, то найдется хотя бы одна точка 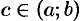 , в которой производная
, в которой производная 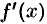 обращается в нуль, т. е.
обращается в нуль, т. е. 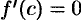 .
.
Так как функция  непрерывна на отрезке
непрерывна на отрезке  , то она достигает на этом отрезке своего наибольшего и наименьшего значений, соответственно,
, то она достигает на этом отрезке своего наибольшего и наименьшего значений, соответственно,  и
и 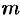 . Если
. Если 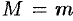 , то функция
, то функция  постоянна на
постоянна на  и следовательно, ее производная
и следовательно, ее производная 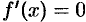 в любой точке отрезка
в любой точке отрезка  .
.
Если 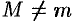 , то функция достигает хотя бы одно из значений
, то функция достигает хотя бы одно из значений  или
или 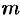 во внутренней точке с интервала
во внутренней точке с интервала  , так как
, так как 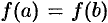 .
.
Пусть, например, функция принимает значение  в точке
в точке 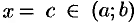 , т. е.
, т. е. 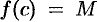 . Тогда для всех
. Тогда для всех 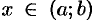 выполняете соотношение
выполняете соотношение

Найдем производную 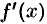 в точке
в точке 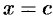 :
:
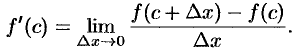
В силу условия (25.1) верно неравенство 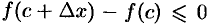 . Если
. Если 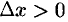 (т. е.
(т. е.  справа от точки
справа от точки 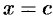 ), то
), то
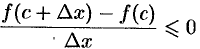 и поэтому
и поэтому 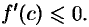
Если 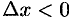 , то
, то
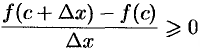 и
и 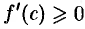 .
.
Таким образом, 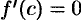 .
.
В случае, когда 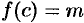 , доказательство аналогичное.
, доказательство аналогичное.
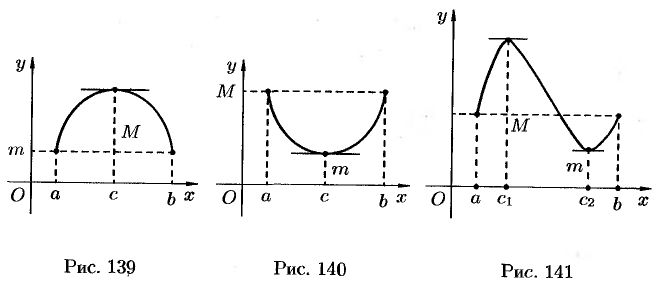
Геометрически теорема Ролля означает, что на графике функции  найдется точка, в которой касательная к графику параллельна оси
найдется точка, в которой касательная к графику параллельна оси  (см. рис. 139 и 140). На рисунке 141 таких точек две.
(см. рис. 139 и 140). На рисунке 141 таких точек две.
Теорема 25.2 (Коши). Если функции  и
и 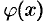 непрерывны на отрезке
непрерывны на отрезке  , дифференцируемы на интервале
, дифференцируемы на интервале  , причем
, причем 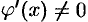 для
для 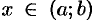 , то найдется хотя бы одна точка
, то найдется хотя бы одна точка 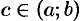 такая, что выполняется равенство
такая, что выполняется равенство 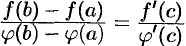 .
.
Отметим, что 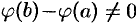 , так как в противном случае по теореме Ролля нашлась бы точка
, так как в противном случае по теореме Ролля нашлась бы точка  , такая, что
, такая, что  , чего не может быть по условию теоремы. Рассмотрим вспомогательную функцию
, чего не может быть по условию теоремы. Рассмотрим вспомогательную функцию
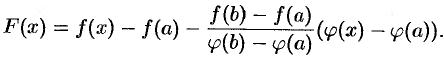
Она удовлетворяет всем условиям теоремы Ролля: непрерывна на отрезке  и дифференцируема на интервале
и дифференцируема на интервале  , так как является
, так как является
линейной комбинацией функций  и
и  ; на концах отрезка она принимает одинаковые значения
; на концах отрезка она принимает одинаковые значения 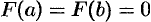 .
.
На основании теоремы Ролля найдется точка 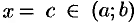 такая, что
такая, что 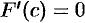 . Но
. Но 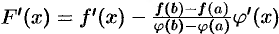 , следовательно,
, следовательно,
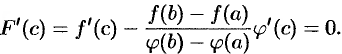
Отсюда следует
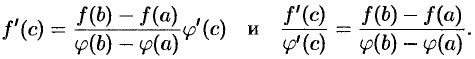
Теорема 25.3 (Лагранж). Если функция  непрерывна на отрезке
непрерывна на отрезке  , дифференцируема на интервале
, дифференцируема на интервале  , то найдется хотя бы одна точка
, то найдется хотя бы одна точка 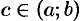 такая, что выполняется равенство
такая, что выполняется равенство
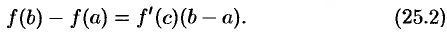
Решение:
Теорему Лагранжа можно рассматривать как частный случай теоремы Коши. Действительно, положив 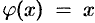 , находим
, находим 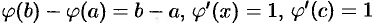 .
.
Подставляя эти значения в формулу 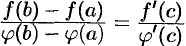 , получаем
, получаем
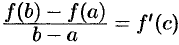 или
или 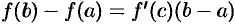 .
.
Полученную формулу называют формулой Лагранжа или формулой о конечном приращении: приращение дифференцируемой функции на отрезке  равно приращению аргумента, умноженному на значение производной функции в некоторой внутренней точке этого отрезка.
равно приращению аргумента, умноженному на значение производной функции в некоторой внутренней точке этого отрезка.
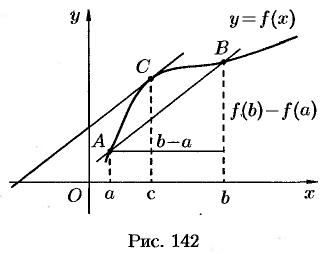
Теорема Лагранжа имеет простой геометрический смысл. Запишем формулу (25.2) в виде
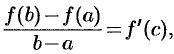
где 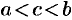 . Отношение
. Отношение 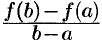 есть угловой коэффициент секущей
есть угловой коэффициент секущей 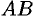 , а величина
, а величина 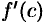 — угловой коэффициент касательной к кривой в точке с абсциссой
— угловой коэффициент касательной к кривой в точке с абсциссой 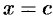 .
.
Следовательно, геометрический смысл теоремы Лагранжа таков: па графике функции  найдется точка
найдется точка 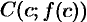 (см. рис. 142), в которой касательная к графику функции параллельна секущей
(см. рис. 142), в которой касательная к графику функции параллельна секущей 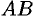 .
.
Следствие 25.1. Если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке.
Пусть 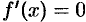 для
для 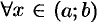 . Возьмем произвольные
. Возьмем произвольные 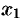 и
и 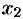 из
из  и пусть
и пусть 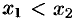 . Тогда по теореме Лагранжа
. Тогда по теореме Лагранжа 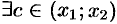 такая, что
такая, что 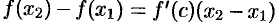 . Но по условию
. Но по условию 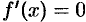 , стало быть,
, стало быть, 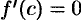 , где
, где 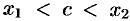 . Поэтому имеем
. Поэтому имеем  , т. е.
, т. е. 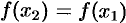 . А так как
. А так как 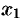 и
и 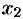 — произвольные точки из интервала
— произвольные точки из интервала  , то
, то 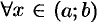 имеем
имеем 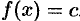 .
.
Следствие 25.2. Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.
Пусть 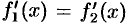 при
при 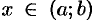 . Тогда
. Тогда 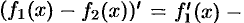
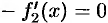 . Следовательно, согласно следствию 25.1, функция
. Следовательно, согласно следствию 25.1, функция 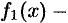
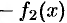 есть постоянная, т.е.
есть постоянная, т.е. 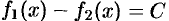 для
для 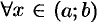 .
.
Пример №25.1.
Доказать, что 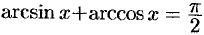 , где
, где 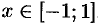 .
.
Решение:
Пусть 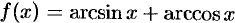 . Тогда
. Тогда 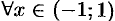 имеем
имеем 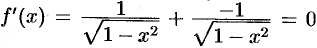 . Отсюда следует, что
. Отсюда следует, что 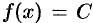 , т.е.
, т.е. 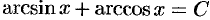 . Положив
. Положив 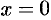 , находим
, находим 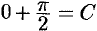 , т. е.
, т. е. 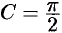 .
.
Поэтому 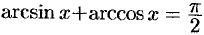 . Это равенство выполняется и при
. Это равенство выполняется и при 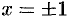 (проверьте!).
(проверьте!).
Аналогично доказывается, что 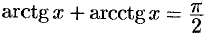 .
.
Формуле Лагранжа можно придать другой вид. Применив теорему Лагранжа к отрезку 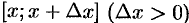 , будем иметь
, будем иметь
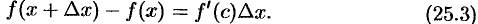
Каждое число 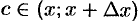 можно записать в виде
можно записать в виде 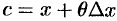 , где
, где 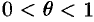 (действительно,
(действительно, 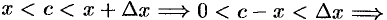
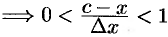 ; положим
; положим 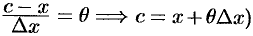 . Формула (25.3) примет вид
. Формула (25.3) примет вид
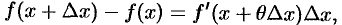
где 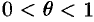 .
.
Используя теорему Лагранжа, можно оценить точность приближенного равенства 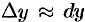 . Сделаем это, считая, что функция
. Сделаем это, считая, что функция  имеет непрерывную вторую производную
имеет непрерывную вторую производную 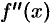 :
:
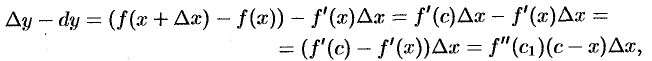
где 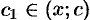 (рис. 143).
(рис. 143).
Итак, 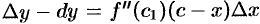 . Пусть
. Пусть 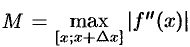 . Так как
. Так как 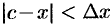 , a
, a 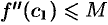 , то получаем оценку
, то получаем оценку 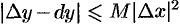 .
.

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Применение дифференциала к приближенным вычислениям |
| Дифференциалы высших порядков |
| Возрастание и убывание функций |
| Максимум и минимум функций |

