Оглавление:
Производные высших порядков неявно заданной функции
Пусть функция  задана неявно в виде уравнения
задана неявно в виде уравнения 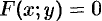 .
.
Продифференцировав это уравнение по  и разрешив полученное уравнение относительно
и разрешив полученное уравнение относительно 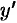 , найдем производную первого порядка (первую производную). Продифференцировав по
, найдем производную первого порядка (первую производную). Продифференцировав по  первую производную, получим вторую производную от неявной функции. В нее войдут
первую производную, получим вторую производную от неявной функции. В нее войдут  ,
,  и
и 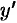 . Подставляя уже найденное значение
. Подставляя уже найденное значение 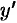 в выражение второй производной, выразим
в выражение второй производной, выразим 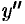 через
через  и
и  .
.
Аналогично поступаем для нахождения производной третьего (и дальше) порядка.
Пример №23.2.
Найти 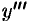 , если
, если 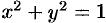 .
.
Решение:
Дифференцируем уравнение 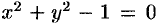 по
по 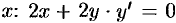 . Отсюда
. Отсюда 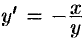 . Далее имеем:
. Далее имеем: 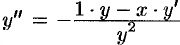 , т. е.
, т. е. 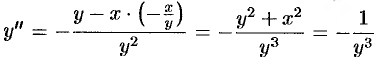 (так как
(так как 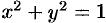 ), следовательно,
), следовательно, 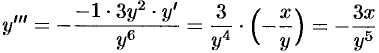 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:

