Механический смысл производной второго порядка
Пусть материальная точка 
движется прямолинейно по закону 
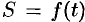. Как уже известно, производная 
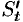равна скорости точки в данный момент времени: 
.
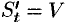Покажем, что вторая производная от пути по времени есть величина ускорения прямолинейного движения точки, т. е.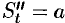 
.
Пусть в момент времени 
скорость точки равна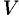 
, а в момент 
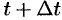— скорость равна 
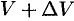, т. е. за промежуток времени 
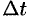скорость изменилась на величину 
.
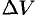Отношение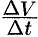 
выражает среднее ускорение движения точки за время 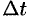. Предел этого отношения при 
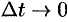называется ускорением точки в данный момент и обозначается буквой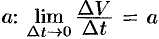 
, т. е. 
.
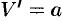Но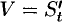 
. Поэтому 
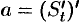, т.е. 
.
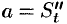На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
