Геометрический и механический смысл производной

Определение производной; ее механический и геометрический смысл. Уравнение касательной и нормали к кривой

Пусть функция определена на некотором интервале 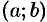. Проделаем следующие операции:

• аргументу 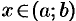дадим приращение ;
• найдем соответствующее приращение функции: ;
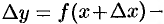
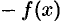• составим отношение приращения функции к приращению аргумента: ;
• найдем предел этого отношения при .

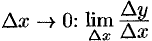Если этот предел существует, то его называют производной функции и обозначают одним из символов .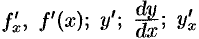

Производной функции в точке называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Итак, по определению

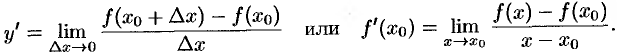
Производная функции есть некоторая функция 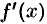, произведенная из данной функции.

Функция , имеющая производную в каждой точке интервала 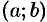, называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.

Значение производной функции в точке 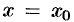обозначается одним из символов: или .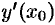

Пример №20.1.

Найти производную функции , .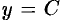

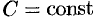Решение:

• Значению даем приращение ;
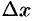• находим приращение функции ;
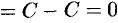• значит, ;
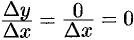• следовательно, .

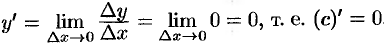Пример №20.2.

Найти производную функции .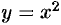

Решение:

• Аргументу даем приращение ;
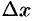• находим ;
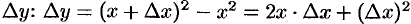• составляем отношение ;
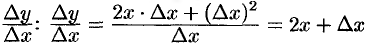• находим предел этого отношения:

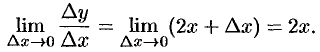
Таким образом, .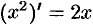

В задаче про скорость прямолинейного движения было получено .

Это равенство перепишем в виде , т. е. скорость прямолинейного движения материальной точки в момент времени есть производная от пути 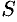по времени . В этом заключается механический смысл производной.

Обобщая, можно сказать, что если функция описывает какой-либо физический процесс, то производная 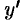есть скорость протекания этого процесса. В этом состоит физический смысл производной.

В задаче про касательную к кривой был найден угловой коэффициент касательной 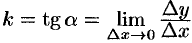. Это равенство перепишем в виде 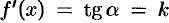, т. е. производная 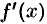в точке равна угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна . В этом заключается геометрический смысл производной.

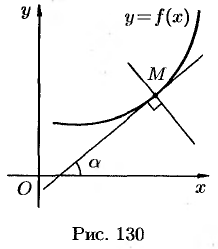
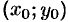Если точка касания имеет координаты (см. рис. 130), то угловой коэффициент касательной есть 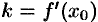. Пользуясь уравнением прямой, проходящей через заданную точку в заданном направлении , можно записать уравнение касательной: .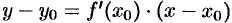

Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.

Так как нормаль перпендикулярна касательной, то ее угловой коэффициент

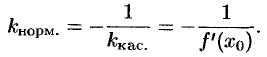
Поэтому уравнение нормали имеет вид (если ).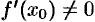

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

• Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

Эквивалентные бесконечно малые функции

Производные основных элементарных функций

Таблица производных. Правила дифференцирования. Формулы дифференцирования

Таблица дифференциалов