Обратная функция
Пусть задана функция  с областью определения
с областью определения 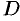 и множеством значений
и множеством значений 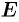 . Если каждому значению
. Если каждому значению 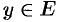 соответствует единственное значение
соответствует единственное значение 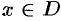 , тo определена функция
, тo определена функция 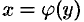 с областью определения
с областью определения 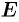 и множеством значений
и множеством значений 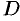 (см. рис. 102). Такая функция
(см. рис. 102). Такая функция 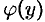 называется обратной к функции
называется обратной к функции  и записывается в следующем виде:
и записывается в следующем виде: 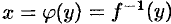 . Про функции
. Про функции  и
и 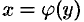 говорят, что они являются взаимно обратными. Чтобы найти функцию
говорят, что они являются взаимно обратными. Чтобы найти функцию 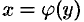 , обратную к функции
, обратную к функции  , достаточно решить уравнение
, достаточно решить уравнение 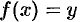 относительно
относительно  (если это возможно).
(если это возможно).
Примеры:
- Для функции
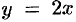 обратной функцией является функция
обратной функцией является функция 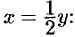
- Для функции
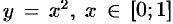 , обратной функцией является
, обратной функцией является 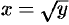 ; заметим, что для функции
; заметим, что для функции 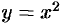 , заданной на отрезке [-1; 1], обратной не существует, т. к. одному значению
, заданной на отрезке [-1; 1], обратной не существует, т. к. одному значению 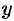 соответствует два значения
соответствует два значения  (так, если
(так, если 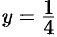 , то
, то 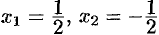 ).
).
Из определения обратной функции вытекает, что функция  имеет обратную тогда и только тогда, когда функция
имеет обратную тогда и только тогда, когда функция  задает взаимно однозначное соответствие между множествами
задает взаимно однозначное соответствие между множествами 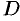 и
и 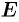 . Отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), го обратная функция также возрастает (убывает).
. Отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), го обратная функция также возрастает (убывает).
Заметим, что функция  и обратная ей
и обратная ей 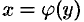 изображаются одной и той же кривой, т. е. графики их совпадают. Если же условиться, что, как обычно, независимую переменную (т. е. аргумент) обозначить через
изображаются одной и той же кривой, т. е. графики их совпадают. Если же условиться, что, как обычно, независимую переменную (т. е. аргумент) обозначить через  , а зависимую переменную через
, а зависимую переменную через 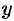 , то функция обратная функции
, то функция обратная функции  запишется в виде
запишется в виде 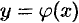 .
.
Это означает, что точка 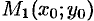 кривой
кривой  становится точкой
становится точкой 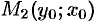 кривой
кривой 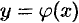 . Но точки
. Но точки 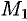 и
и 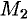 симметричны относительно прямой
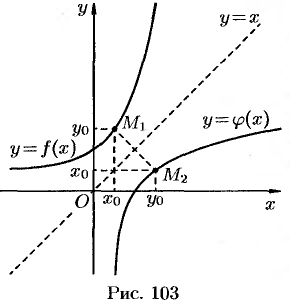
симметричны относительно прямой 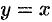 (см. рис. 103). Поэтому графики взаимно обратных функций
(см. рис. 103). Поэтому графики взаимно обратных функций  и
и 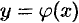 симметричны относительно биссектрисы первого и третьего координатных углов.
симметричны относительно биссектрисы первого и третьего координатных углов.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Основные теоремы о пределах |
| Признаки существования пределов |
| Сложная функция |
| Основные элементарные функции |

