Оглавление:
Произведение матриц
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Произведением матрицы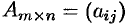 
на матрицу 
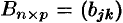называется матрица 
такая, что
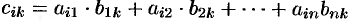, где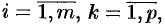 
т. e. элемент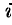 
-й строки и 
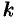-го столбца матрицы произведения 
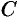равен сумме произведений элементов 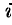-й строки матрицы 
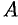на соответствующие элементы 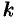-го столбца матрицы 
.
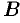Получение элемента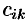 
схематично изображается так:
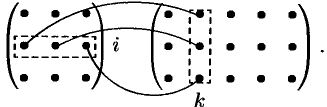
Если матрицы 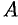и 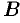квадратные одного размера, то произведения 
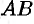и 
всегда существуют. Легко показать,, что 
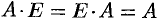, где 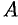— квадратная матрица, 
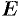— единичная матрица того же размера.
Пример №1.5.
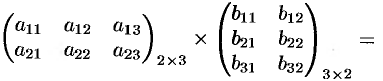
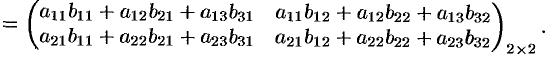
Дополнительный пример №1.6.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Преобразование Лапласа |
| Операционный метод решения линейных дифференциальных уравнений и их систем |
| Свойства определителей |
| Невырожденные матрицы |
