Оглавление:
Операционный метод решения линейных дифференциальных уравнений и их систем
Пусть требуется найти частное решение линейного дифференциального уравнения с постоянными коэффициентами
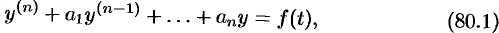
удовлетворяющее начальным условиям
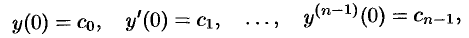
где 
— заданные числа.
Будем считать, что искомая функция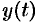 
вместе с ее рассматриваемыми производными и функция 
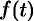являются оригиналами.
Пусть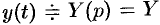 
и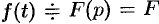 
. Пользуясь свойствами дифференцирования оригинала и линейности, перейдем в уравнении (80.1) от оригиналов к изображениям:
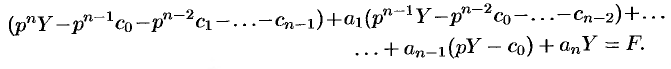
Полученное уравнение называют операторным (или уравнением в изображениях). Разрешим его относительно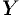 
:
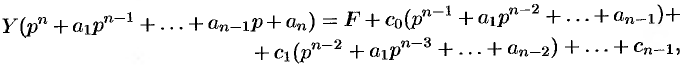
т. е.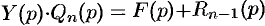 
, где 
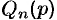и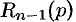 
—алгебраические многочлены от 
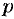степен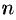и 
и 
соответственно.
Из последнего уравнения находим
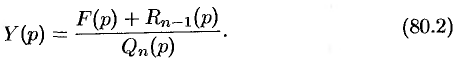
Полученное равенство называют операторным решением дифференциального уравнения (80.1). Оно имеет более простой вид, если все начальные условия равны нулю, т. е.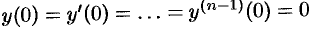 
. В этом случае 
.
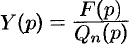Находя оригинал 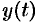, соответствующий найденному изображению (80.2), получаем, в силу теоремы единственности, частное решение дифференциального уравнения (80.1).
Замечание. Полученное решение 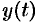во многих случаях оказывается справедливым при всех значениях 
(а не только при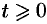 
).
Пример №80.1.
Решить операционным методом дифференциальное уравнение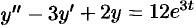 
при условиях 
.
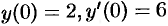Решение:
Пусть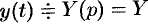 
. Тогда
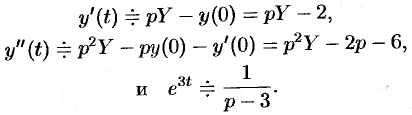
Подставляя эти выражения в дифференциальное уравнение, получаем операторное уравнение: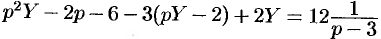 
. Отсюда 
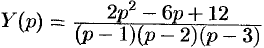. Находим 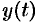. Можно разбить дробь на сумму простейших 
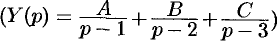, но так как корни знаменателя 
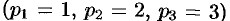простые, то удобно воспользоваться второй теоремой разложения (формула (79.1)), в которой
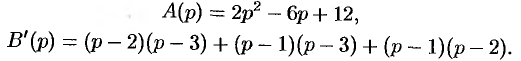
Получаем:
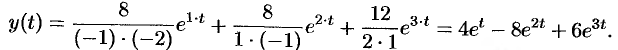
Дополнительные примеры:
Приложения
Правила дифференцирования
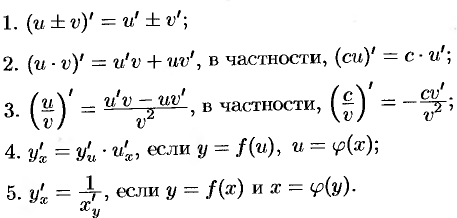
Формулы дифференцирования
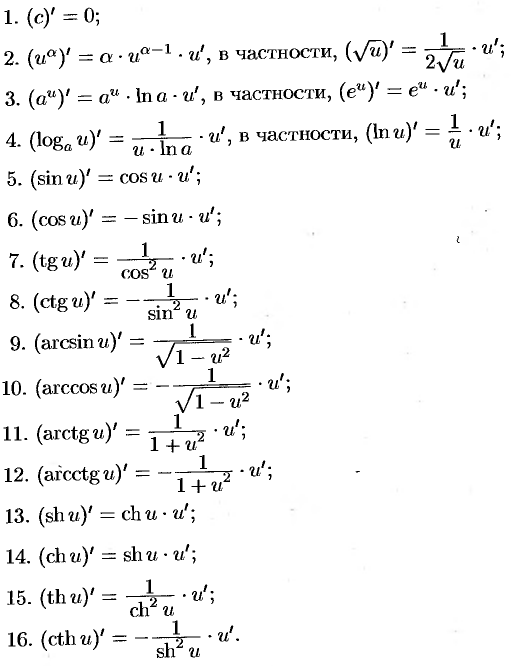
Таблица основных интегралов
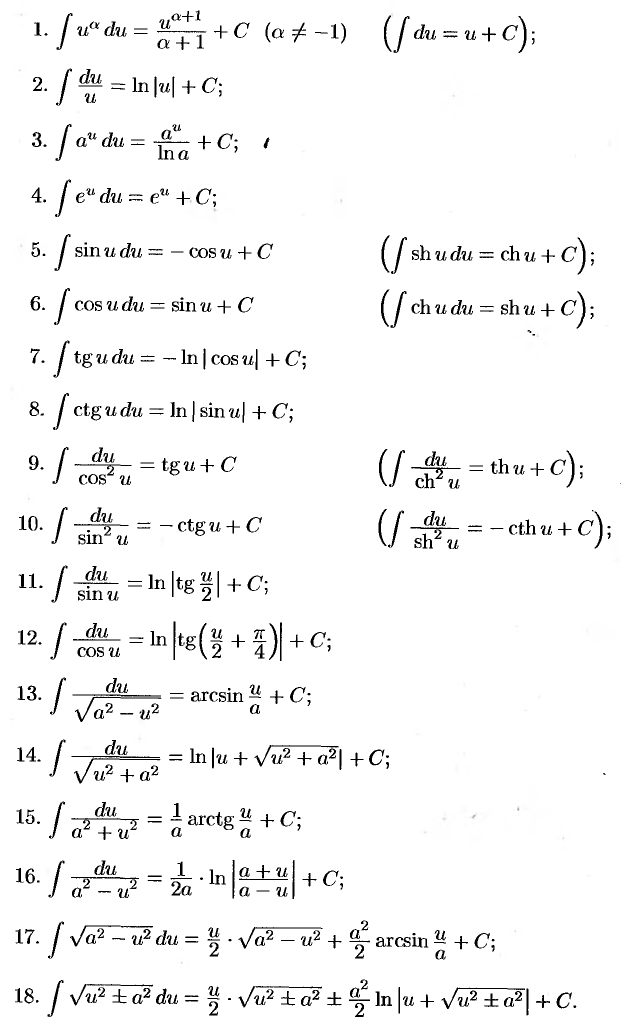
Таблица разложений в ряд Маклорена некоторых элементарных функций
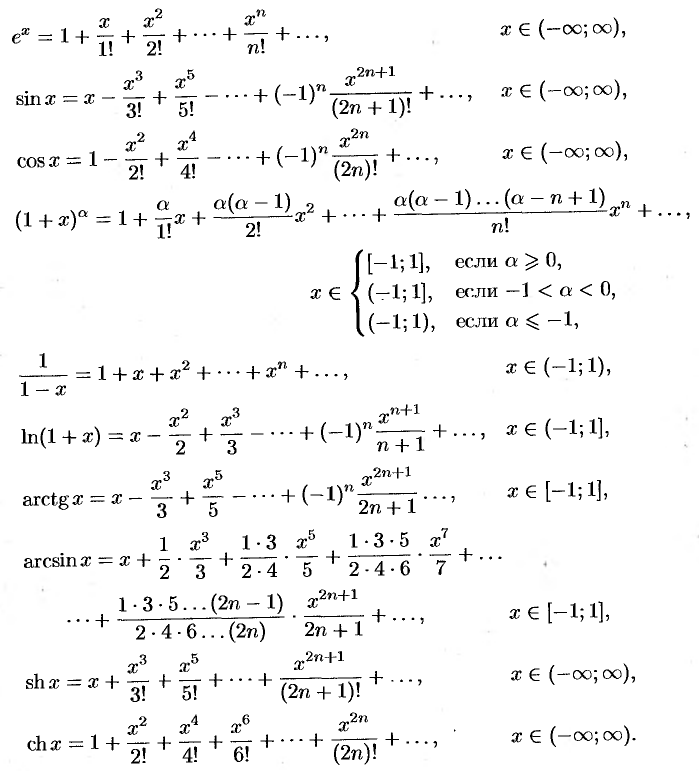
Таблица оригиналов и изображений
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Понятие вычета и основная теорема о вычетах |
| Преобразование Лапласа |
| Произведение матриц |
| Свойства определителей |
