Оглавление:
Преобразование Лапласа
Оригиналы и их изображения
Основными первоначальными понятиями операционного исчисления являются понятия функции-оригинала и функции-изображения.
Пусть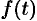 
— действительная функция действительного переменного 
(под будем понимать время или координату).
Функция 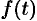называется оригиналом, если она удовлетворяет следующим условиям:
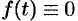при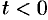 
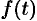.- — кусочно-непрерывная при
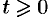, т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси таких точек лишь конечное число. - Существуют такие числа
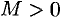и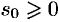 
, что для всех выполняется неравенство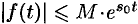 
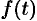, т. е. при возрастании функция может возрастать не быстрее некоторой показательной функции. Число 
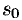называется показателем роста .
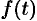Условия 1-3 выполняются для большинства функций, описывающих различные физические процессы.
Первое условие означает, что процесс начинается с некоторого момента времени; удобнее считать, что в момент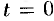 
. Третьему условию удовлетворяют ограниченные функции (для них можно положить 
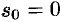), степенные 
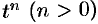и другие (для функций вида 
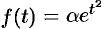условие 3 не выполняется). Не является оригиналом, например, функция 
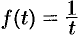(не удовлетворяет второму условию).
Замечание. Функция 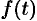может быть и комплексной функцией действительно переменного, т. е. иметь вид 
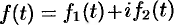она считается оригиналом, если действительные функци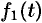и 
и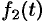 
являются оригиналами.
Изображением оригинала 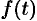называется функция 
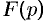комплексного переменного 
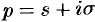, определяемая интегралом
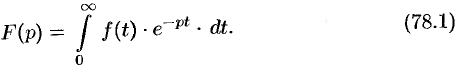
Операцию перехода от оригинала 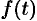к изображению 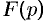называют преобразованием Лапласа. Соответствие между оригиналом 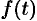и изображением 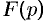записывается в виде 
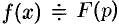или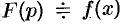 
(принято оригиналы обозначать малыми буквами, а их изображения — соответствующими большими буквами).
Теорема 78.1 (существование изображения). Для всякого оригинала 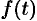изображение 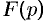существует (определено) в полуплоскости 
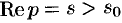, где 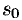— показатель роста функции 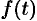, причем функция 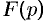является аналитической в этой полуплоскости 
.
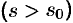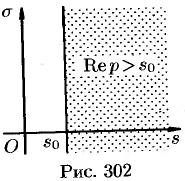
Докажем первую часть теоремы. Пусть 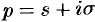произвольная точка полуплоскости 
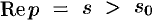(см. рис. 302). Учитывая, что 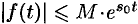, находим:
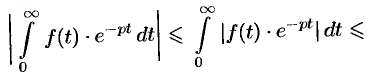
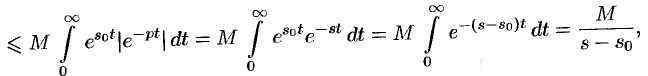
так как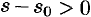 
и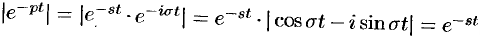 
. Таким образом,
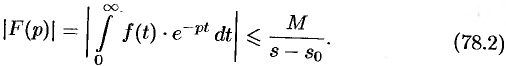
Отсюда вытекает абсолютная сходимость интеграла (78.1), т. е. изображение 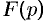существует и однозначно в полуплоскости .
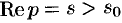Следствие 78.1 (необходимый признак существования изображения). Если функция 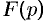является изображением функции 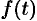, то
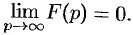
Это утверждение непосредственно вытекает из неравенства (78.2), когда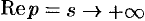 
.
Так как 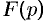— аналитическая функция в полуплоскости 
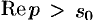, то 
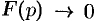при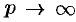 
по любому направлению. Отсюда, в частности, следует, что функции 
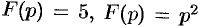не могут быть изображениями.
Отметим, что из аналитичности функции 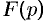следует, что все ее особые точки должны лежать левее прямой 
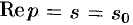или на самой этой прямой. Функция 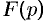, не удовлетворяющая этому условию, не является изображением функции 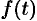. Не является изображением, например, функция 
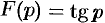(ее особые точки расположены на всей оси 
).
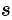Теорема 78.2 (о единственности оригинала). Если функция 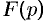служит изображением двух оригиналов 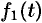и 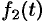, то эти оригиналы совпадают друг с другом во всех точках, в которых они непрерывны.
(Примем без доказательства.)
Пример №78.1.
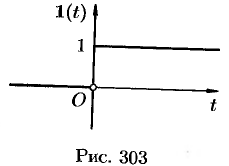
Найти изображение единичной функции Хевисайда
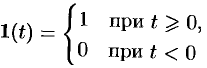
(см. рис. 303).
Решение:
По формуле (78.1) при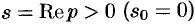 
находим:
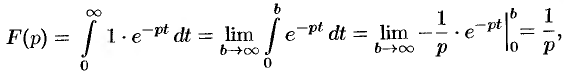
т.е.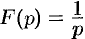 
, или, в символической записи, 
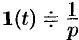, или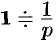 
.
Замечание. В дальнейшем функцию-оригинал будем кратко записывать в виде 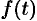, подразумевая, что
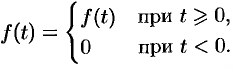
Дополнительные примеры:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Ряды в комплексной плоскости |
| Понятие вычета и основная теорема о вычетах |
| Операционный метод решения линейных дифференциальных уравнений и их систем |
| Произведение матриц |
