Оглавление:
Основные элементарные функции комплексного переменного
Определим основные элементарные функции комплексного переменного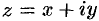 
.
Показательная функция
Показательная функция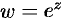 
определяется формулой
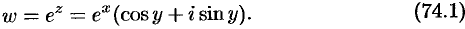
Положив в этом равенстве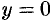 
, устанавливаем, что для действительных значений 
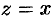показательная функция 
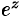совпадает с показательной функцией действительного переменного: 
.
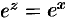Показательная функция 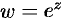обладает «известным» свойством: 
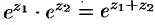. Действительно, по правилу умножения комплексных чисел («модули перемножаются, а аргументы складываются», п. 28.3), имеем:
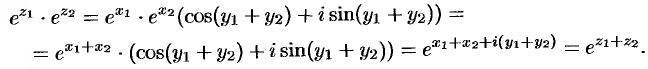
Аналогично можно убедиться в справедливости свойств: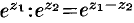 
, 
.
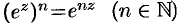Учитывая, что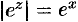 
, а 
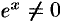, утверждаем, что показательная функция 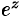нигде в нуль не обращается, т. е. 
.
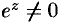Исходя из определения (74.1), легко убедиться, что
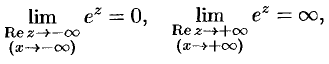
выражение 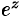при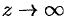 
не имеет смысла.
Положив в равенстве (74.1)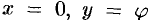 
, получим классическую формулу Эйлера 
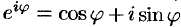. С ее помощью, в частности, можно представить тригонометрическую форму комплексного числа 
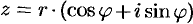в более компактной форме 
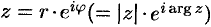, называемой показательной формой комплексного числа (см. п. 27.3)
Показательная функция комплексного переменного обладает и специфическим свойством: она является периодической с мнимым основным периодом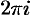 
.
Действительно,
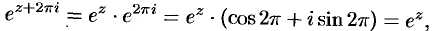
т.е.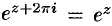 
. Отметим, что 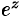не всегда больше нуля. Например, 
.
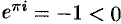Логарифмическая функция
Эта функция определяется как функция, обратная показательной: число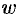 
называется логарифмом числа 
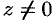, если 
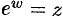, обозначается 
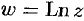. Так как значения показательной функции 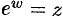всегда отличны от нуля, то логарифмическая функция 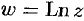определена на всей плоскости 
, кроме точки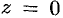 
(стало быть, имеет) смысл и выражение 
).
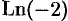Положив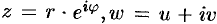 
, получим, согласно определению логарифмической функции, 
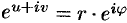, или 
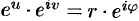. Отсюда имеем:
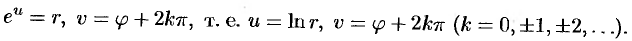
Следовательно,
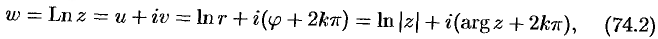
т.е.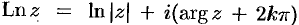 
или, 
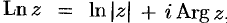, где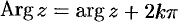 
.
Формула (74.2) показывает, что логарифмическая функция комплексного переменного имеет бесчисленное множество значений, т. е. 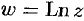— многозначная функция.
Однозначную ветвь этой функции можно выделить, подставив в формулу (74.2) определенное значение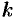 
. Положив 
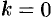, получим однозначную функцию, которую называют главным значением логарифма 
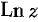и обозначают символом 
:
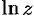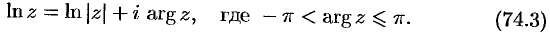
Если — действительное положительное число, то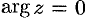 
и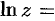 
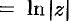, т. е. главное значение логарифма действительного положительного числа совпадает с обычным натуральным логарифмом этого числа.
Формулу (74.2) можно переписать так: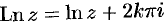 
.
Из формулы (74.2) следует, что логарифмическая функция 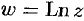обладает известными свойствами логарифма действительного переменного:
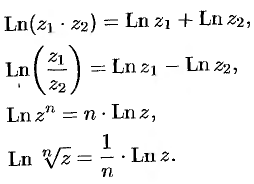
Докажем, например, первое свойство:
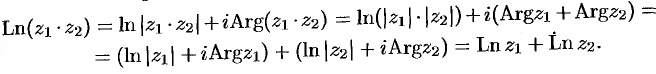
Пример №74.2.
Вычислить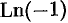 
и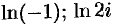 
.
Решение:
Для числа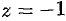 
имеем 
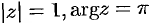. Следовательно, 
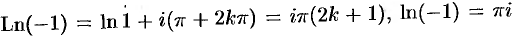(формулы (74.2) и (74.3));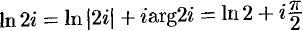 
Степенная функция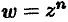 
Если 
— натуральное число, то степенная функция определяется равенством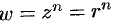 
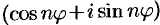. Функция 
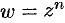— однозначная. Если 
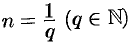, то в этом случае
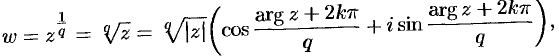
где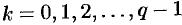 
.
Здесь функция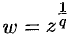 
есть многозначная (
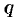-значная) функция. Однозначную ветвь этой функции можно получить, придав 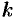определенное значение, например .
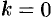Если 
где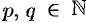 
, то степенная функция определяется равенством
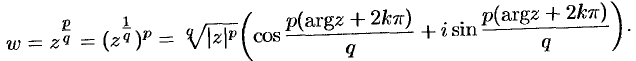
Функция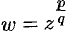 
— многозначная.
Степенная функция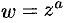 
с произвольным комплексным показателем 
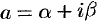определяется равенством
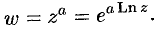
Функция 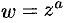определена для всех 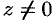, является многозначной функцией. Так, 
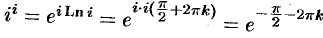, где 
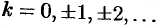При 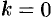имеем: 
.
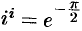Тригонометрические функции
Тригонометрические функция комплексного аргумента 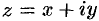определяются равенствами
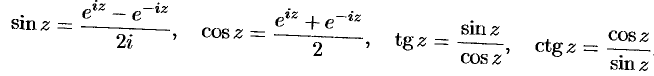
При действительных эти определения приводят к тригонометрическим функциям действительного переменного. Так, при ()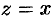
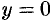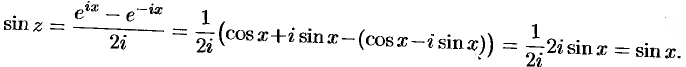
Тригонометрические функции комплексного переменного сохраняют многие свойства тригонометрических функций действительного переменного. В частности,
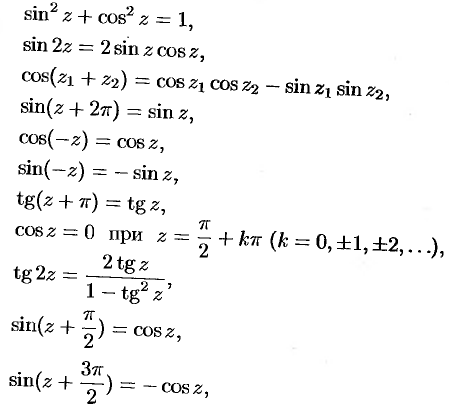
и т.д. Докажем, например, первое свойство:
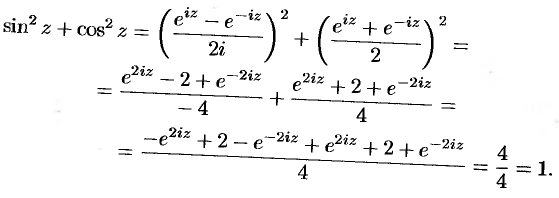
Отметим, что тригонометрические функци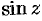и 
и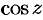 
в комплексной плоскости неограничены:
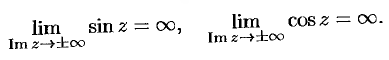
Так, например,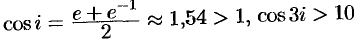 
.
Гиперболические функции
Эти функции определяются равенствами
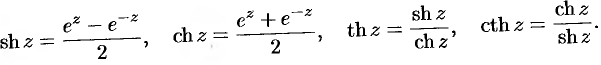
Легко заметить связь между гиперболическими и тригонометрическими функциями. Заменяя в указанных функциях на 
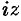, получим:
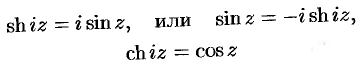
(а также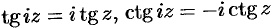 
).
Пользуясь этими равенствами, можно получить ряд формул, связывающих гиперболические функции. Так, заменяя в формуле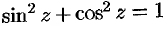 
тригонометрические функции гиперболическими, получим
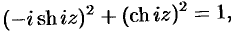
или —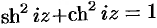 
. Так как здесь — любое комплексное число, то 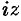можно заменить на ; получим формулу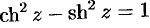 
. Приведем еще ряд формул:
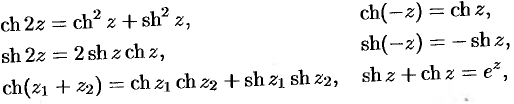
и т.д.
Из определения гиперболических функций следует, что функци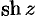и 
и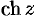 
периодические с периодом 
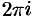; функци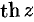и 
и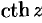 
имеют период 
.
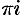Обратные тригонометрические и гиперболические функции
Число 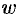называется арксинусом числа , если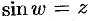 
, и обозначается 
.
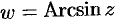Используя определение синуса, имеем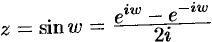 
или 
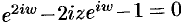. Отсюда 
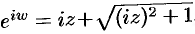, т. е. 
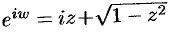(перед корнем можно не писать знак 
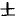, так как 
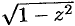имеет два значения). Тогда 
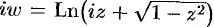, или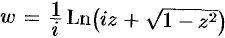 
. Таким образом,
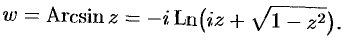
Функция 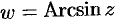многозначна (бесконечнозначна). Аналогично определяются другие обратные тригонометрические функции. Можно показать, что
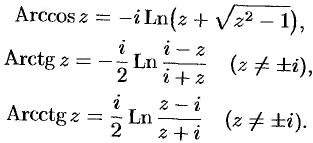
Функции, обратные гиперболическим, обозначаются-соответственно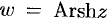 
(ареасинус), 
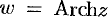(ареакосинус), 
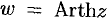(apea-тангенс), 
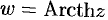(ареакотангенс).
Обратные гиперболические функции имеют следующие выражения:
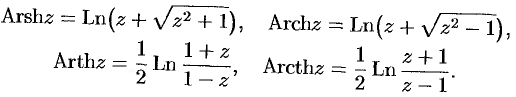
Все эти функции бесконечнозначны.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Векторные дифференциальные операции второго порядка |
| Предел и непрерывность функции комплексного переменного |
| Ряды в комплексной плоскости |
| Понятие вычета и основная теорема о вычетах |
