Векторные дифференциальные операции второго порядка
После применения оператора Гамильтона к скалярному или векторному полю получается новое поле, к которому можно снова применить этот оператор. В результате получаются дифференциальные операции второго порядка. Нетрудно убедиться, что имеется лишь пять дифференциальных операций второго порядка: 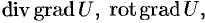
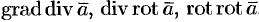 .
.
(Понятно, что операция 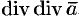 , например, не имеет смысла:
, например, не имеет смысла: 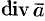 — скаляр, говорить о дивергенции скаляра, т. е. о
— скаляр, говорить о дивергенции скаляра, т. е. о 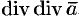 , бессмысленно.)
, бессмысленно.)
Запишем явные выражения для дифференциальных операций второго порядка, используя оператор Гамильтона. Заметим при этом, что, оператор действует только на множитель, расположенный непосредственно за оператором.
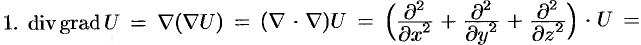
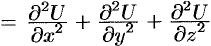 . Правая часть этого равенства называется оператором Лапласа скалярной функции
. Правая часть этого равенства называется оператором Лапласа скалярной функции 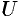 и обозначается
и обозначается 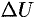 . Таким образом,
. Таким образом,
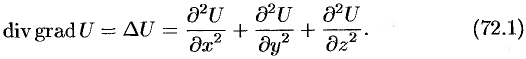
Дифференциальное уравнение Лапласа 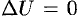 играет важную роль в различных разделах математической физики. Решениями уравнения Лапласа являются так называемые гармонические функции.
играет важную роль в различных разделах математической физики. Решениями уравнения Лапласа являются так называемые гармонические функции.
Замечание. К равенству (72.1) можно прийти, введя в рассмотрение скалярный оператор дельта:
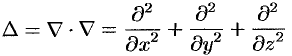
(который тоже называют оператором Лапласа).
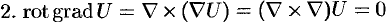 , так как векторное произведение двух одинаковых векторов равно нулю (пуль-вектор). Это означает, что поле градиента есть поле безвихревое.
, так как векторное произведение двух одинаковых векторов равно нулю (пуль-вектор). Это означает, что поле градиента есть поле безвихревое.
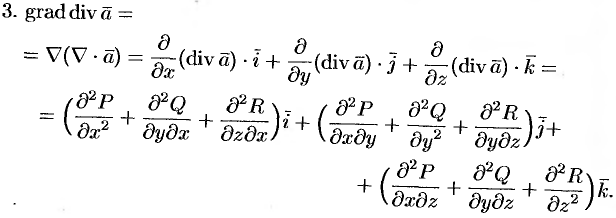
 , так как смешанное произведение трех векторов, из которых два одинаковые, равно нулю. Это означает, что поле вихря — соленоидальное.
, так как смешанное произведение трех векторов, из которых два одинаковые, равно нулю. Это означает, что поле вихря — соленоидальное.
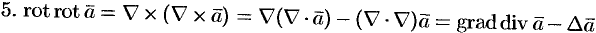 , так как двойное векторное произведение обладает свойством
, так как двойное векторное произведение обладает свойством
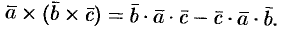
Здесь 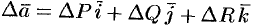 — векторная величина, полученная на результате применения оператора Лапласа к вектору
— векторная величина, полученная на результате применения оператора Лапласа к вектору  .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Поток векторного поля |
| Векторные дифференциальные операции первого порядка |
| Предел и непрерывность функции комплексного переменного |
| Основные элементарные функции комплексного переменного |

