Периодические функции. Периодические процессы
При изучении разнообразных периодических процессов, т. е. процессов, которые через определенный промежуток времени повторяются (встречаются в радиотехнике, электронике, теории упругости, теории и практике автоматического регулирования и т. д.), целесообразнее разлагать периодические функции, описывающие эти процессы, не в степенной ряд, а в так называемый тригонометрический ряд.
Напомним, что функция 
, определенная на множестве 
, называется периодической (см. п. 14.3) с периодом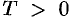 
, если при каждом 
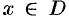значение 
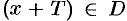и выполняется равенство 
.
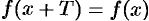Для построения графика периодической функции периода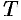 
достаточно построить его на любом отрезке длины 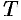и периодически продолжить его во всю область определения.
Отметим основные свойства периодической функции.
- Алгебраическая сумма периодических функций, имеющих один и тот же период 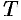, есть периодическая функция с периодом .
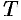- Если функция
имеет период 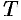, то функция 
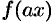имеет период 
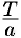действительно, 
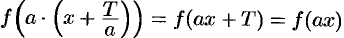. - Если функция имеет период 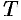и интегрируема на отрезке
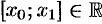, то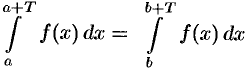 
при любых 
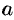и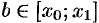 
.
Пусть, например,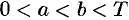 
, тогда
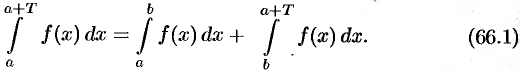
С другой стороны,
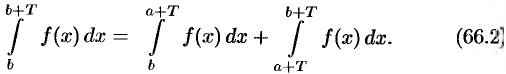
По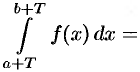 
(подстановка 
) 
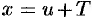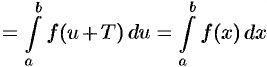
Подставляем полученный результат в (66.2) и, сравнивая с (66.1), имеем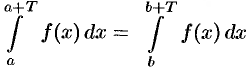 
.
В частности,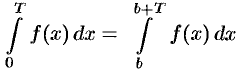 
.
Простейшими периодическими функциями являются тригонометрические функци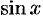и 
и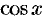 
. Период этих функций равен 
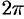, т. е. 
.
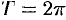Простейшим периодическим процессом (движением) является простое гармоническое колебание (движение), описываемое функцией
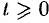, где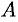 
— амплитуда колебания, 
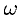— частота, 
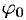— начальная фаза.
Функцию такого вида (и ее график) называют простой гармоникой. Основным периодом функции (66.3) является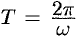 
, т. е. одно полное колебание совершается за промежуток времени 
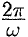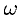( показывает, сколько колебаний совершает точка в течение 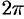единиц времени).
Проведем преобразование функции (66.3):
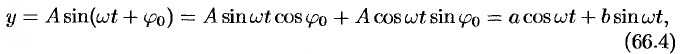
где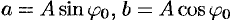 
. Отсюда видно, что простое гармоническое колебание описывается периодическими функциям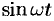и 
и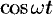 
.
Сложное гармоническое колебание, возникающее в результате наложения конечного (или бесконечного) числа простых гармоник, также описывается функциями вида 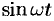и 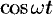. Так, функция
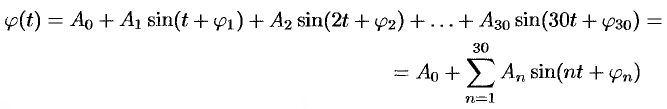
или, что равносильно, функция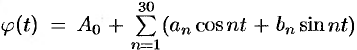 
задает сложное гармоническое колебание. Так как период первой гармоники есть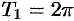 
, второй 
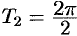, третьей 
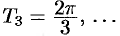, тридцатой 
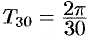, а период функции 
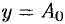(«пулевая гармоника») есть любое число, то функция 
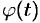имеет период, равный 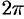, т. е. .
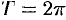Понятно, что при наложении простых гармоник получаем периодическую функцию, описывающую сложное периодическое колебание (периодический процесс).
Возникает вопрос: всякую ли периодическую функцию, описывающую периодический процесс, можно представить в виде суммы простых гармоник вида (66.3) или (66.4)? Если да, то как найти неизвестные параметры (коэффициенты) каждой из этих гармоник? Ответим сначала на второй вопрос, а потом и на первый.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Свойства степенных рядов |
| Ряды Тейлора и Маклорена |
| Разложение в ряд фурье периодических функций с периодом 2п |
| Поверхности и линии уровня скалярного поля |
