Оглавление:
Общий достаточный признак сходимости знакопеременных рядов
Знакочередующийся ряд является частным случаем знакопеременного ряда. Числовой ряд 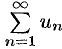 содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным.
содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным.
Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.
Теорема 61.2. Пусть дан знакопеременный ряд
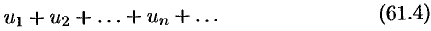
Если сходится ряд
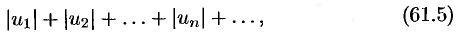
составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд (61.4).
Рассмотрим вспомогательный ряд, составленный из членов рядом (61.4) и (61.5):
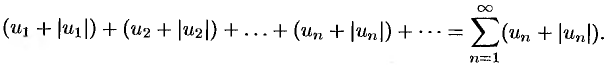
Очевидно, что 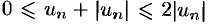 для всех
для всех 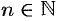 . Но ряд
. Но ряд 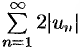 сходится в силу условия теоремы и свойства 1 числовых рядов (п. 59.1) . Следовательно, на основании признака сравнения (п. 59.3) сходится и ряд
сходится в силу условия теоремы и свойства 1 числовых рядов (п. 59.1) . Следовательно, на основании признака сравнения (п. 59.3) сходится и ряд 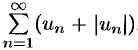 . Поскольку данный знакопеременный ряд (61.4) представляет собой разность двух сходящихся рядов
. Поскольку данный знакопеременный ряд (61.4) представляет собой разность двух сходящихся рядов
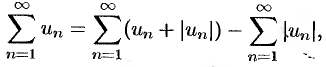
то, на основании свойства 2 числовых радов, он (ряд (61.4)) сходится.
Отметим, что обратное утверждение несправедливо: если сходится ряд (61.4), то это не означает, что будет сходиться ряд (61.5).
Пример №61.2.
Исследовать сходимость ряда 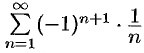 .
.
Решение:
Это знакочередующийся ряд, для которого выполнены условия признака Лейбница. Следовательно, указанный ряд сходится. Однако ряд, составленный из модулей членов данного ряда, т. е.
ряд
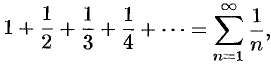
расходится (гармонический ряд).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Интегральный признак Коши |
| Знакочередующиеся ряды. Признак Лейбница |
| Сходимость степенных рядов |
| Свойства степенных рядов |

