Оглавление:
Достаточные признаки сходимости знакопостоянных рядов
Необходимый признак сходимости не дает, вообще говоря, возможности судить о том, сходится ли данный ряд или нет. Сходимость расходимость ряда во многих случаях можно установить с помощью так называемых достаточных признаков.
Рассмотрим некоторые из них для знакоположительных pядов, т. е. рядов с неотрицательными членами (знакоотрицательный ряд переходит в знакоположительный путем умножения его на (—1), что, как известно, не влияет на сходимость ряда).
Признаки сравнения рядов
Сходимость или расходимость знакоположительного ряда часто устанавливается путем сравнения его с другим («эталонным») рядом о котором известно, сходится он или нет. В основе такого сравнения лежат следующие теоремы.
Теорема 60.1. Пусть даны два знакоположительных ряда

и

Если для всех 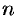 выполняется неравенство
выполняется неравенство

то из сходимости ряда (60.2) следует сходимость ряда (60.1), из расходимости ряда (60.1) следует расходимость ряда (60.2).
Обозначим 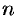 -е частичные суммы рядов (60.1) и (60.2) соответственно через
-е частичные суммы рядов (60.1) и (60.2) соответственно через 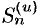 и
и 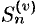 . Из неравенства (60.3) следует, что
. Из неравенства (60.3) следует, что

Пусть ряд (60.2) сходится и его сумма равна 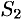 . Тогда
. Тогда 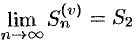 .
.
Члены ряда (60.2) положительны, поэтому 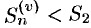 и, следовательно, с учетом неравенства (60.4),
и, следовательно, с учетом неравенства (60.4), 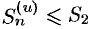 . Таким образом, последовательность
. Таким образом, последовательность 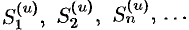 монотонно возрастает
монотонно возрастает 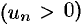 и ограничена сверху числом
и ограничена сверху числом 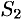 . По признаку существования предела (см. теорема 15.3) последовательность
. По признаку существования предела (см. теорема 15.3) последовательность 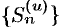 имеет предел
имеет предел 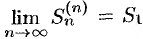 , т. е. ряд (60.1) сходится.
, т. е. ряд (60.1) сходится.
Пусть теперь ряд (60.1) расходится. Так как члены ряда неотрицательны, в этом случае имеем 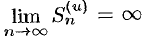 . Тогда, с учетом неравенства (60.4), получаем
. Тогда, с учетом неравенства (60.4), получаем 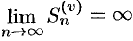 , т. е. ряд (60.2) расходится.
, т. е. ряд (60.2) расходится.
Замечание. Теорема 60.1 справедлива и в том случае, когда неравенство (60.3) выполняется не для всех членов рядов (60.1) и (60.2), а начиная с некоторого номера 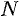 . Это вытекает из свойства 3 числовых рядов (см. п. 59.1).
. Это вытекает из свойства 3 числовых рядов (см. п. 59.1).
Теорема 60.2 (предельный признак сравнения). Пусть даны два знакоположительных ряда (60.1) и (60.2). Если существует конечный, отличный от 0, предел 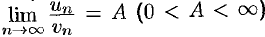 , то ряды (60.1) и (60.2) сходятся или расходятся одновременно.
, то ряды (60.1) и (60.2) сходятся или расходятся одновременно.
По определению предела последовательности (см. п. 15.2) для всех 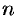 , кроме, возможно, конечного числа их, для любого
, кроме, возможно, конечного числа их, для любого 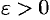 выполняется неравенство
выполняется неравенство 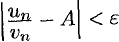 , или
, или
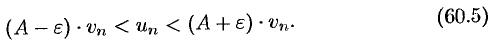
Если ряд (60.1) сходится, то из левого неравенства (60.5) и теоремы 60.1 вытекает, что ряд 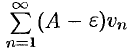 также сходится. Но тогда, согласно свойству 1 числовых рядов (см. п. 59.1), ряд (60.2) сходится.
также сходится. Но тогда, согласно свойству 1 числовых рядов (см. п. 59.1), ряд (60.2) сходится.
Если ряд (60.1) расходится, то из правого неравенства (60.5), теоремы 60.1, свойства 1 вытекает, что и ряд (60.2) расходится.
Аналогично, если ряд (60.2) сходится (расходится), то сходящимся (расходящимся) будет и ряд (60.1).
Пример №60.1.
Исследовать на сходимость ряд 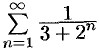 .
.
Решение:
Сравним данный ряд с рядом геометрической прогрессии 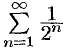 , который сходится
, который сходится 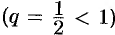 . Имеем
. Имеем 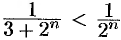 . Следовательно, данный ряд сходится.
. Следовательно, данный ряд сходится.
Благодаря этой странице вы научитесь сами решать такие примеры, на ней содержится полный курс лекций с примерами решения:
Дополнительные примеры:

