Оглавление:
Необходимый признак сходимости числового ряда. Гармонический ряд
Нахождение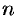 
-й частичной суммы 
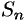и ее предела для произвольного ряда во многих случаях является непростой задачей. Поэтому для выяснения сходимости ряда устанавливают специальные признаки сходимости. Первым из них, как правило, является необходимый признак сходимости.
Теорема 59.1. Если ряд (59.1) сходится, то его общий член un стремится к нулю, т. е.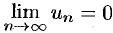 
.
Пусть ряд (59.1) сходится и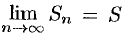 
. Тогда и 
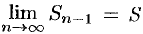(при 
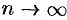и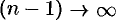 
). Учитывая, что 
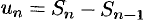при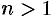 
, получаем:
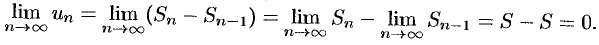
Следствие 59.1 (достаточное условие расходимости ряда). Если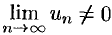 
или этот предел не существует, то ряд расходится.
Действительно, если бы ряд сходился, то (по теореме) 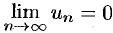. Но это противоречит условию. Значит, ряд расходится.
Пример №59.2.
Исследовать сходимость ряда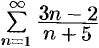 
.
Решение:
Ряд 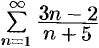расходится, т. к.
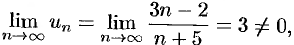
т. е. выполняется достаточное условие расходимости ряда.
Дополнительный пример №59.3.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Интегрирование нормальных систем |
| Ряд геометрической прогрессии |
| Достаточные признаки сходимости знакопостоянных рядов |
| Признак Даламбера |
