Оглавление:
Уравнения Лагранжа и Клеро
Рассмотрим дифференциальные уравнения, неразрешенные относительно производной. К ним, в частности, относятся уравнения Лагранжа и Клеро.
Уравнение Лагранжа
Уравнение вида
где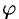 
и 
— и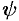звестные функции от 
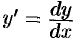называется уравнением Лагранжа.
Введем вспомогательный параметр, положив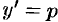 
. Тогда уравнение (48.25) примет вид
Дифференцируя по 
, получим:
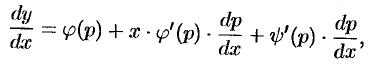
т. е.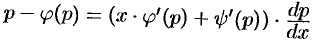 
, или
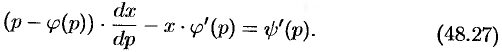
Уравнение (48.27) есть линейное уравнение относительно неизвестной функции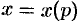 
. Решив его, найдем:
Исключая параметр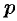 
из уравнений (48.26) и (48.28), получаем общий интеграл уравнения (48.25) в виде 
.
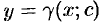Отметим, что, переходя к уравнению (48.27), мы делили на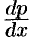 
. При этом могли быть потеряны решения, для которых 
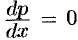, т. е.
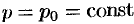. Это значение 
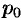является корнем уравнения 
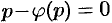(см. (48.27)).
Решение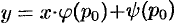 
является особым для уравнения (48.25) (см. понятие особого решения в п. 48.2).
Уравнение Клеро
Рассмотрим частный случай уравнения Лагранжа при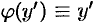 
. Уравнение (48.25) принимает вид
и называется уравнением Клеро.
Положив 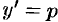, получаем:
Дифференцируя по , имеем:
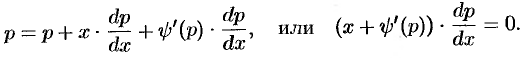
Если 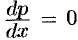, то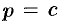 
. Поэтому, с учетом (48.30), ДУ (48.29) имеет общее решение
Если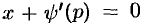 
, то получаем частное решение уравнения в параметрической форме:
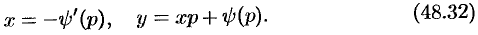
Это решение — особое решение уравнения Клеро: оно не содержится в формуле общего решения уравнения.
Пример №48.13.
Решить уравнение Клеро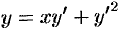 
.
Решение:
Общее решение, согласно формуле (48.31), имеет вид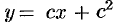 
. Особое решение уравнения получаем согласно формулам (48.32) в виде 
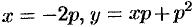. Отсюда, следует: 
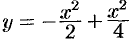, т. е. 
.
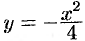На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Метод вариации произвольных постоянных |
| Уравнение в полных дифференциалах интегрирующий множитель |
| Уравнения, допускающие понижение порядка |
| Линейные однородные ДУ второго порядка |
