Оглавление:
Метод Лагранжа (метод вариации произвольной постоянной)
Уравнение (48.11) интегрируется следующим образом.
Рассмотрим соответствующее уравнение без правой части, т. е. уравнение 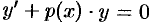 . Оно называется линейным однородным ДУ первого порядка. В этом уравнении переменные делятся:
. Оно называется линейным однородным ДУ первого порядка. В этом уравнении переменные делятся:
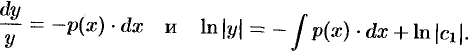
Таким образом, 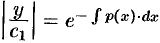 , т.е.
, т.е.
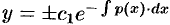 или
или 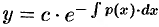 , где
, где 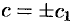 .
.
Метод вариации произвольной постоянной состоит в том, что постоянную 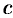 в полученном решении заменяем функцией
в полученном решении заменяем функцией 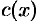 , т. е. полагаем
, т. е. полагаем 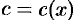 . Решение уравнения (48.11) ищем в виде
. Решение уравнения (48.11) ищем в виде

Находим производную:
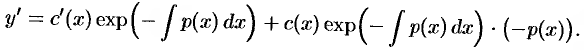
Подставляем значения  и
и 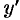 в уравнение (48.11):
в уравнение (48.11):
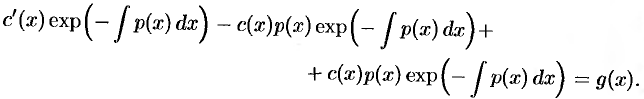
Второе и третье слагаемые взаимно уничтожаются, и уравнение примет вид
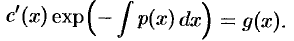
Следовательно,
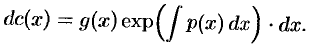
Интегрируя, находим:
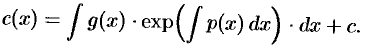
Подставляя выражение 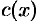 в равенство (48.14), получим общее решение ДУ (48.11):
в равенство (48.14), получим общее решение ДУ (48.11):
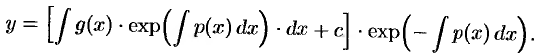
Естественно, та же формула была получена методом Бернулли (cр. с (48.13)).
Пример №48.9.
Решить пример 48.8 методом Лагранжа.
Решение:
Решаем уравнение 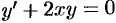 . Имеем
. Имеем 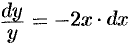 , или
, или 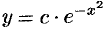 . Заменяем
. Заменяем 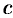 на
на 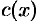 , т. е. решение ДУ
, т. е. решение ДУ 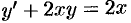 ищем в виде
ищем в виде 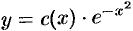 . Имеем
. Имеем

Тогда
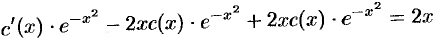 , т.е.
, т.е. 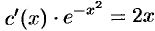 , или
, или 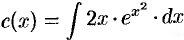 , или
, или 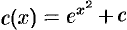 . Поэтому
. Поэтому 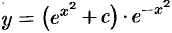 , или
, или 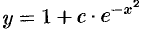 — общее решение данного уравнения.
— общее решение данного уравнения.
Замечание. Уравнение вида 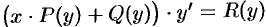 , где
, где 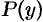 ,
, 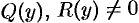 — заданные функции, можно свести к линейному, если
— заданные функции, можно свести к линейному, если  считать функцией, а
считать функцией, а  — аргументом:
— аргументом: 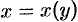 . Тогда, пользуясь равенством
. Тогда, пользуясь равенством 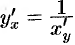 , получаем
, получаем 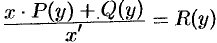 , т. е.
, т. е. 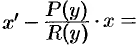
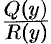 — линейное относительно
— линейное относительно  уравнение. Его решение ищем в виде
уравнение. Его решение ищем в виде 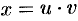 , где
, где 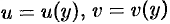 — две неизвестные функции.
— две неизвестные функции.
Дополнительный пример №48.10.
Уравнение Я. Бернулли
Уравнение вида
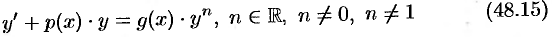
называется уравнением Бернулли. Покажем, что его можно привести к линейному.
Если 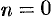 , то ДУ (48.15) — линейное, а при
, то ДУ (48.15) — линейное, а при 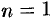 — с разделяющимися переменными.
— с разделяющимися переменными.
В общем случае, разделив уравнение (48.15) на 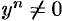 , получим:
, получим:
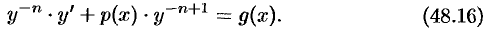
Обозначим 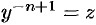 . Тогда
. Тогда 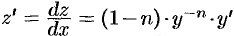 . Отсюда находим
. Отсюда находим 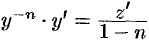 . Уравнение (48.16) принимает вид
. Уравнение (48.16) принимает вид
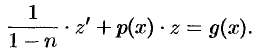
Последнее уравнение является линейным относительно  . Решение его известно. Таким образом, подстановка
. Решение его известно. Таким образом, подстановка 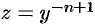 сводит уравнение (48.15) к линейному. На практике ДУ (48.15) удобнее искать методом И. Бернулли в виде
сводит уравнение (48.15) к линейному. На практике ДУ (48.15) удобнее искать методом И. Бернулли в виде 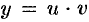 (не сводя его к линейному).
(не сводя его к линейному).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Однородные дифференциальные уравнения |
| Линейные уравнения Бернулли |
| Уравнение в полных дифференциалах интегрирующий множитель |
| Уравнения Лагранжа и Клеро |

