Оглавление:
Дифференцирование неявной функции
Функция 
называется неявней, если она задается уравнением
неразрешенным относительно 
. Найдем частные производные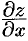 
и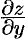 
неявной функции , заданной уравнением (44.11). Для этого, подставив в уравнение вместо функцию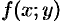 
, получим тождество
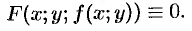
Частные производные по 
и по 
функции, тождественно равной нулю, также равны нулю:
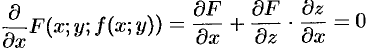( — считаем постоянным),
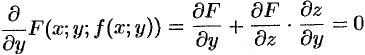( — считаем постоянным),
откуда
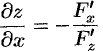и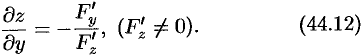 
Замечания.
а) Уравнение вида (44.11) не всегда определяет одну переменную как неявную функцию двух других. Так, уравнение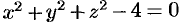 
определяет функци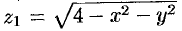и 
и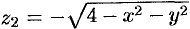 
, определенные в круге 
, 
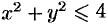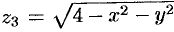, определенную в полукруге 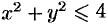при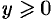 
и т. д., а уравнение 
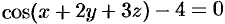не определяет никакой функции.
Имеет место теорема существования неявной функции двух переменных: если функция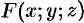 
и ее производные 
, 
, 
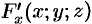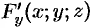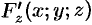определены и непрерывны в некоторой окрестности точки 
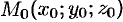, причем 
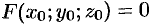, a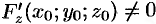 
, то существует окрестность точки 
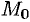, в которой уравнение (44.11) определяет единственную функцию , непрерывную и дифференцируемую в окрестности точки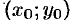 
и закую, что 
.
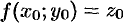б) Неявная функция 
одной переменной задается уравнением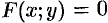 
. Можно показать, что в случае, если удовлетворены условия существования неявной функции одной переменной (имеется теорема, аналогичная вышеуказанной), то производная неявной функции находится по формуле
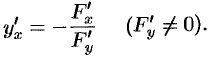
Пример №44.6.
Найти частные производные функции , заданной уравнением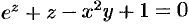 
.
Решение:
Здесь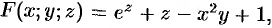 
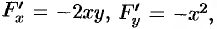
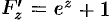. По формулам (44.12) имеем: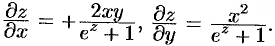 
Дополнительный пример №44.7.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Производная сложной функции |
| Инвариантность формы полного дифференциала |
| Касательная плоскость и нормаль к поверхности |
| Необходимые и достаточные условия экстремума |
