Инвариантность формы полного дифференциала
Используя правило дифференцирования сложной функции, можно показать, что полный дифференциал обладает свойством инвариантности: полный дифференциал функции  сохраняет один и тот же вид независимо от того, являются ли аргументы независимыми переменными или функциями независимых переменных.
сохраняет один и тот же вид независимо от того, являются ли аргументы независимыми переменными или функциями независимых переменных.
Пусть  , где
, где  и
и  — независимые переменные. Тогда полный дифференциал (1-го порядка) функции имеет вид
— независимые переменные. Тогда полный дифференциал (1-го порядка) функции имеет вид
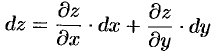
(формула (44.5)).
Рассмотрим сложную функцию  , где
, где 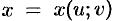 ,
, 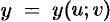 , т. е. функцию
, т. е. функцию 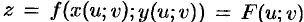 , где
, где 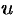 и
и 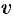 — независимые переменные. Тогда имеем:
— независимые переменные. Тогда имеем:
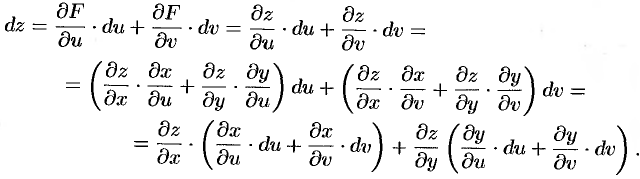
Выражения в скобках представляют собой полные дифференциалы 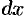 и
и 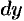 функций
функций 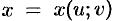 и
и 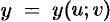 . Следовательно, и в этом случае,
. Следовательно, и в этом случае,
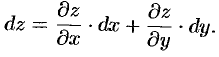
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Дифференциалы высших порядков |
| Производная сложной функции |
| Дифференцирование неявной функции |
| Касательная плоскость и нормаль к поверхности |

