Оглавление:
Применение полного дифференциала к приближенным вычислениям
Из определения дифференциала функции 
следует, что при достаточно малых 
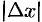и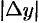 
имеет место приближенное равенство
Так как полное приращение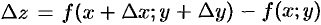 
, равенство (44.6) можно переписать в следующем виде:
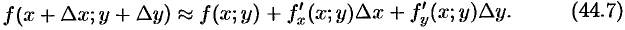
Формулой (44.7) пользуются в приближенных расчетах.
Пример №44.3.
Вычислить приближенно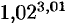 
.
Решение:
Рассмотрим функцию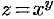 
. Тогда 
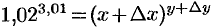, где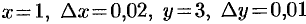 
. Воспользуемся формулой (44.7), предварительно найдя 
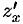и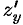 
: 
, 
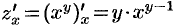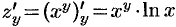. Следовательно, 
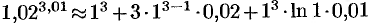, т. е.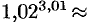 
.
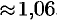Для сравнения: используя микрокалькулятор, находим:
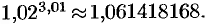
Отметим, что с помощью полного дифференциала можно найти: границы абсолютной и относительной погрешностей в приближенных вычислениях; приближенное значение полного приращения функции и т. д.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Частные производные высших порядков |
| Дифференцируемость и полный дифференциал функции |
| Дифференциалы высших порядков |
| Производная сложной функции |
