Оглавление:
Частные производные первого порядка и их геометрическое истолкование
Пусть задана функция 
. Так как 
и 
— независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной приращение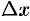 
, сохраняя значение неизменным. Тогда 
получит приращение, которое называется частным приращением по и обозначается 
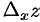. Итак,
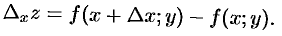
Аналогично получаем частное приращение по :
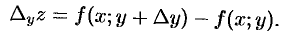
Полное приращение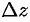 
функции определяется равенством
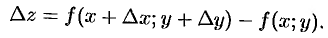
Если существует предел
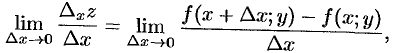
то он называется частной производной функции в точке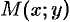 
по переменной и обозначается одним из символов:
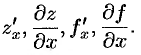
Частные производные по в точке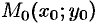 
обычно обозначают символами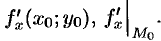 
Аналогично определяется и обозначается частная производная от по переменной :
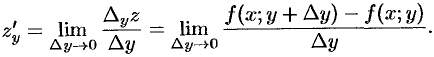
Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции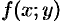 
находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно или считается постоянной величиной).
Пример №44.1.
Найти частные производные функции
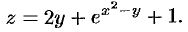
Решение:
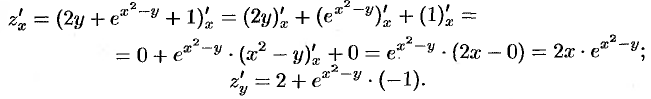
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
