Оглавление:
Предел функции
Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывности, аналогично случаю функции одной переменной. Введем понятие окрестности точки. Множество всех точек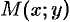 
плоскости, координаты которых удовлетворяют неравенству 
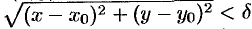, называется 
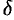-окрестностью точки 
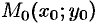. Другими словами, 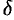-окрестность точки 
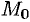— это все внутренние точки круга с центром 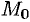и радиусом 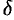(см. рис. 205).
Пусть функция 
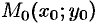определена в некоторой окрестности точки , кроме, быть может, самой этой точки. Число 
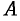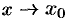называется пределом функции при 
и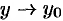 
(или, что то же самое, при 
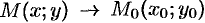), если для любого 
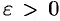существует 
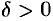такое, что для всех 
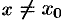и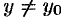 
и удовлетворяющих неравенству 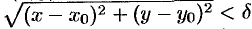выполняется неравенство 
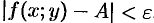. Записывают:
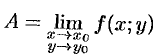или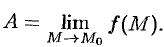 
Из определения следует, что если предел существует, то он не зависит от пути, по которому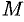 
стремится к 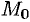(число таких направлений бесконечно; для функции одной переменной 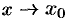по двум направлениям: справа и слева!)
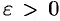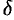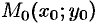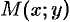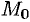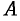Геометрический смысл предела функции двух переменных состоит в следующем. Каково бы ни было число , найдется -окрестность точки , что во всех ее точках , отличных от , аппликаты соответствующих точек поверхности отличаются от числа по модулю меньше, чем на 
.
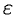Пример №43.1.
Найти предел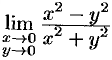 
.
Решение:
Будем приближаться к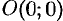 
по прямой 
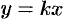, где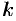 
— некоторое число. Тогда
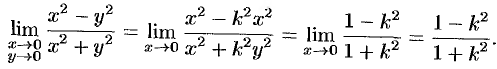
Функция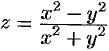 
в точке 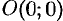предела не имеет, т. к. при разных значениях 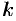предел функции не одинаков (функция имеет различные предельные значения).
Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной (см. п. 17.3). Это означает, что справедливы утверждения: если функци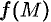и 
и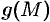 
определены на множестве 
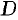и имеют в точке 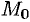этого множества пределы 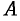и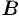 
соответственно, то и функции 
, 
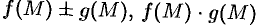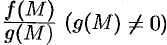имеют в точке 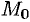пределы, которые соответственно равны 
.
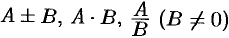На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Работа переменной силы |
| Приближенное вычисление определенного интеграла |
| Непрерывность функции двух переменных |
| Свойства функций, непрерывных в ограниченной замкнутой области |
