Оглавление:
Приближенное вычисление определенного интеграла
Пусть требуется найти определенный интеграл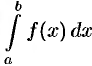 
от непрерывной функции 
. Если можно найти первообразную 
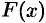функции , то интеграл вычисляется по формуле Ньютона-Лейбница:
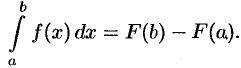
Но отыскание первообразной функции иногда весьма сложно; кроме того, как известно, не для всякой непрерывной функции ее первообразная выражается через элементарные функции. В этих и других случаях (например, функция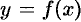 
задана графически или таблично) прибегают к приближенным формулам, с помощью которых определенный интеграл находится с любой степенью точности.
Рассмотрим три наиболее употребительные формулы приближенного вычисления определенного интеграла — формулу прямоугольников, формулу трапеций, формулу парабол (Симпсона), основанные на геометрическом смысле определенного интеграла.
Формула прямоугольников
Пусть на отрезке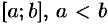 
, задана непрерывная функция . Требуется вычислить интеграл 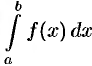, численно равный площади соответствующей криволинейной трапеции. Разобьем основание этой трапеции, т. е. отрезок 
, на 
равных частей (отрезков) длины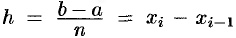 
(шаг разбиения) с помощью точек 
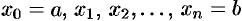. Можно записать, что 
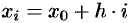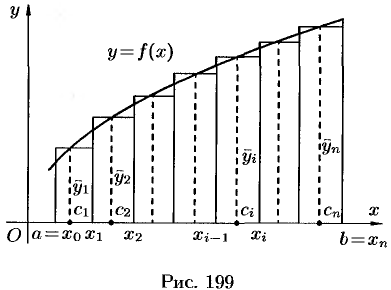
, где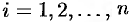 
(см. рис. 199).
В середине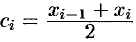 
каждого такого отрезка построим ординату 
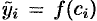графика функции 
. Приняв эту ординату за высоту, построим прямоугольник с площадью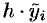 
.
Тогда сумма площадей всех прямоугольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение искомого определенного интеграла
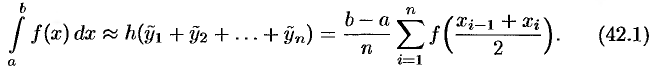
Формула (42.1) называется формулой средних прямоугольников.
Абсолютная погрешность приближенного равенства (42.1) оценивается с помощью следующей формулы:
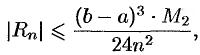
где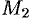 
— наибольшее значение 
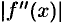на отрезке ,
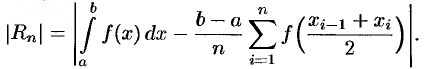
Отметим, что для линейной функции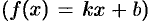 
формула (42.1) дает точный ответ, поскольку в этом случае 
.
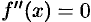Формула трапеций
Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.
Разобьем отрезок на равных частей длины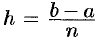 
. Абсциссы точек деления 
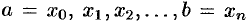(рис. 200). Пусть 
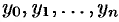— соответствующие им ординаты графика функции. Тогда
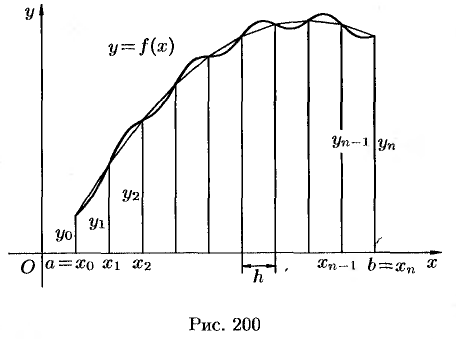
расчетные формулы для этих значений примут вид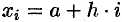 
, 
, ; .
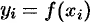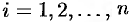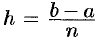Заменим кривую ломаной линией, звенья которой соединяют концы ординат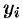 
и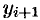 
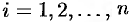(). Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями 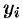, 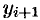и высотой :
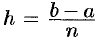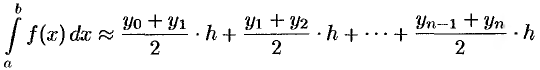
или
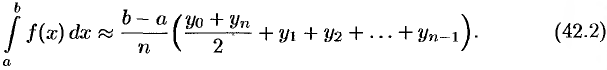
Формула (42.2) называется формулой, трапеций.
Абсолютная погрешность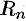 
приближения, полученного по формуле трапеций, оценивается с помощью формулы 
,
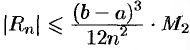где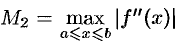 
. Снова для линейной функции 
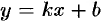формула (42.2) — точная.
Формула парабол (Симпсона)
Если заменить график функции на каждом отрезке 
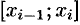разбиения не отрезками прямых, как в методах трапеций и прямоугольников, а дугами парабол, то получим более точную формулу приближенного вычисления интеграла .
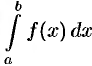Предварительно найдем площадь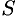 
криволинейной трапеции, ограниченной сверху графиком параболы 
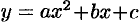, сбоку — прямыми 
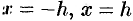и снизу — отрезком 
.
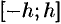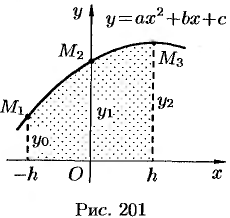
Пусть парабола проходит через три точки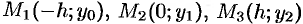 
, где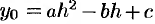 
— ордината параболы в точке 
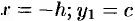— ордината параболы в точке 
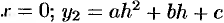— ордината параболы в точке 
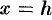(см. рис. 201). Площадь 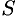равна
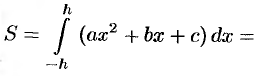
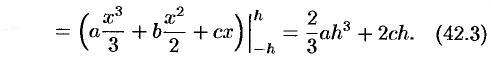
Выразим эту площадь через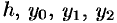 
. Из равенств для ординат 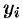находим, что 
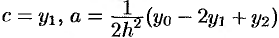. Подставляя эти значения 
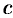и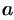 
в равенство (42.3), получаем
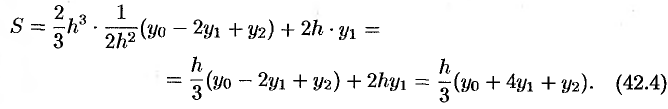
Получим теперь формулу парабол для вычисления интеграла .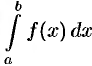
Для этого отрезок разобьем на 
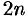равных частей (отрезков) длиной 
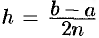точками 
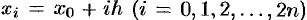. В точках деления 
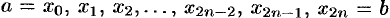вычисляем значения подынтегральной функции : 
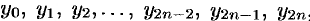, где 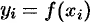(см. рис. 202).
Заменяем каждую пару соседних элементарных криволинейных трапеций с основаниями, равными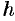 
, одной элементарной параболической трапецией с основанием, равным 
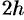. На отрезке 
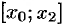парабола проходит через три точки 
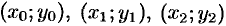. Используя формулу (42.4), находим
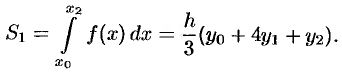
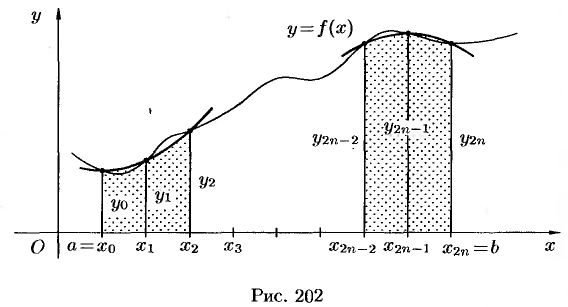
Аналогично находим
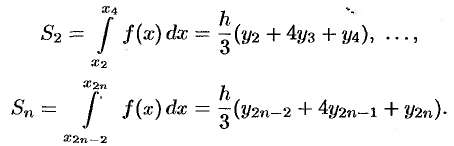
Сложив полученные равенства, имеем
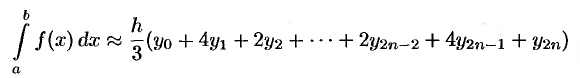
или
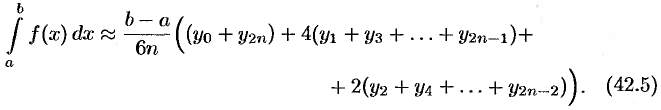
Формула (42.5) называется формулой парабол (или Симпсона).
Абсолютная погрешность вычисления по формуле (42.5) оценивается соотношением
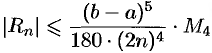, где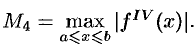 
Отметим, что формула (42.5) лает точное значение интеграла 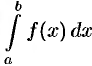во всех случаях, когда — многочлен, степень которого меньше или равна трем (тогда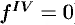 
).
Пример №42.1.
Вычислить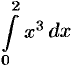 
, разбив отрезок интегрирования [0; 2] на 4 части.
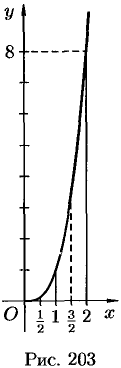
Решение:
Имеем: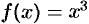 
,
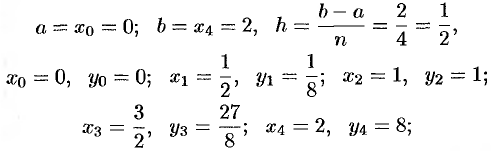
(см. рис. 203)
а) по формуле прямоугольников:
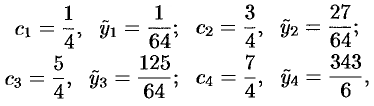
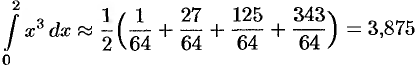, т.е.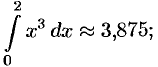 
б) по формуле трапеции:
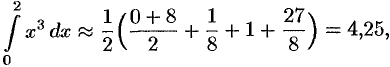т.е.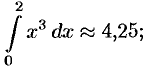 
в) по формуле парабол:
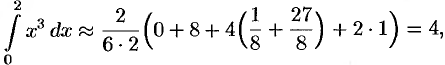т.е.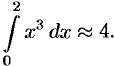 
Точное значение интеграла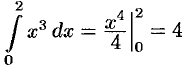 
.
Абсолютные погрешности соответствующих формул таковы:
.
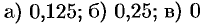На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Вычисление площади поверхности вращения |
| Работа переменной силы |
| Предел функции двух переменных |
| Непрерывность функции двух переменных |
