Оглавление:
Интеграл с бесконечным промежутком интегрирования (несобственный интеграл I рода)
Пусть функция  непрерывна на промежутке
непрерывна на промежутке 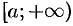 . Если существует конечный предел
. Если существует конечный предел 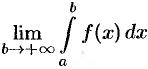 , то его называют несобственным интегралом первого рода и обозначают
, то его называют несобственным интегралом первого рода и обозначают 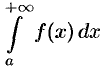 .
.
Таким образом, по определению
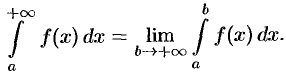
В этом случае говорят, что несобственный интеграл 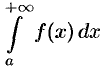 сходится. Если же указанный предел не существует или он бесконечен, то говорят, что интеграл
сходится. Если же указанный предел не существует или он бесконечен, то говорят, что интеграл 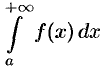 расходится.
расходится.
Аналогично определяется несобственный интеграл на промежутке 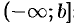 :
:
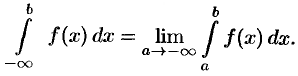
Несобственный интеграл с двумя бесконечными пределами определяется формулой
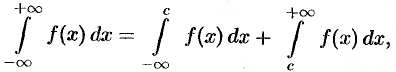
где 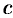 — произвольное число. В этом случае интеграл слева сходится лишь тогда, когда сходятся оба интеграла справа. Отметим, что если непрерывная функция
— произвольное число. В этом случае интеграл слева сходится лишь тогда, когда сходятся оба интеграла справа. Отметим, что если непрерывная функция 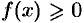 на промежутке
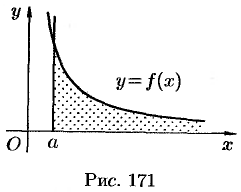
на промежутке 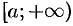 и интеграл
и интеграл 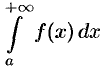 сходится, то он выражает площадь бесконечно длинной криволинейной трапеции (см. рис. 171).
сходится, то он выражает площадь бесконечно длинной криволинейной трапеции (см. рис. 171).
Пример №40.1.
Вычислить несобственные интегралы или установить их расходимость: 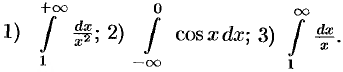
Решение:
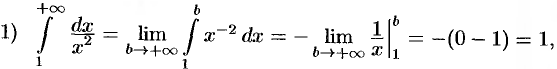 интеграл сходится;
интеграл сходится;
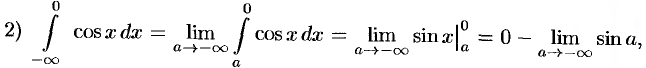 интеграл расходится, так как при
интеграл расходится, так как при 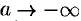 предел
предел 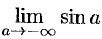 не существует.
не существует.
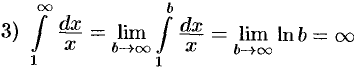 , интеграл расходится.
, интеграл расходится.
В некоторых задачах нет необходимости вычислять интеграл; достаточно лишь знать, сходится ли он или нет.
Приведем без доказательства некоторые признаки сходимости.
Теорема 40.1 (признак сравнения). Если на промежутке 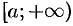 непрерывные функции
непрерывные функции  и
и 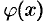 удовлетворяют условию
удовлетворяют условию 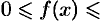
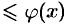 , то из сходимости интеграла
, то из сходимости интеграла 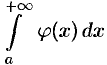 следует сходимость интеграла
следует сходимость интеграла 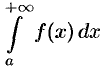 , а из расходимости интеграла
, а из расходимости интеграла 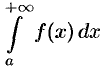 следует расходимость интеграла
следует расходимость интеграла 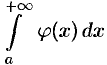 .
.
Дополнительные примеры:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Основные свойства определенного интеграла |
| Вычисления определенного интеграла |
| Интеграл от разрывной функции |
| Схемы применения определенного интеграла |

