Оглавление:
Вычисления определенного интеграла
Формула ньютона-лейбница
Простым и удобным методом вычисления определенного интеграла 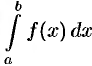 от непрерывной функции является формула Ньютона-Лейбница:
от непрерывной функции является формула Ньютона-Лейбница:
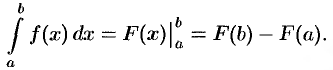
Применяется этот метод во всех случаях, когда может быть найдена первообразная функции 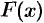 для подынтегральной функции
для подынтегральной функции  .
.
Например, 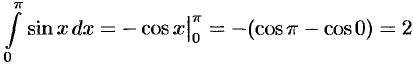 .
.
При вычислении определенных интегралов широко используется метод замены переменной и метод интегрирования по частям.
Интегрирование подстановкой (заменой переменной)
Пусть для вычисления интеграла 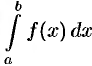 от непрерывной функции сделана подстановка
от непрерывной функции сделана подстановка 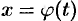 .
.
Теорема 39.1. Если:
1) функция 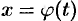 и ее производная
и ее производная 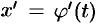 непрерывны при
непрерывны при 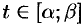 ;
;
2) множеством значений функции 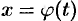 при
при 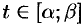 является отрезок
является отрезок  ;
;
3) 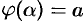 и
и 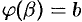 , то
, то
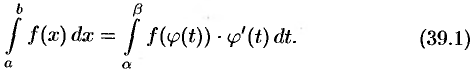
Пусть 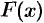 есть первообразная для
есть первообразная для  на отрезке
на отрезке  . Тогда по формуле Ньютона-Лейбница
. Тогда по формуле Ньютона-Лейбница 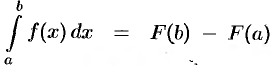 . Так как
. Так как 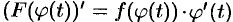 , то
, то 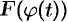 является первообразной для функции
является первообразной для функции 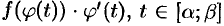 . Поэтому по формуле Ньютона-Лейбница имеем
. Поэтому по формуле Ньютона-Лейбница имеем
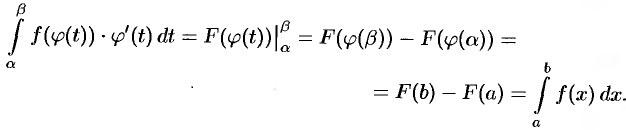
Формула (39.1) называется формулой замены переменной в определенном интеграле.
Отметим, что:
1) при вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется;
2) часто вместо подстановки 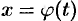 применяют подстановку
применяют подстановку 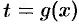 ;
;
3) не следует забывать менять пределы интегрирования при замене переменных!
Пример №39.1.
Вычислить 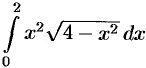 .
.
Решение:
Положим 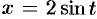 , тогда
, тогда 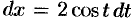 . Если
. Если 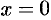 , то
, то 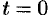 ; если
; если 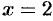 , то
, то 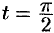 . Поэтому
. Поэтому
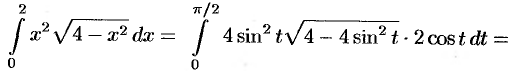
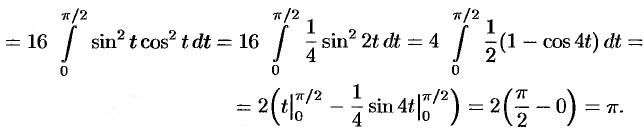
Интегрирование по частям
Теорема 39.2. Если функции 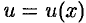 и
и 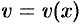 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке  , то имеет место формула
, то имеет место формула
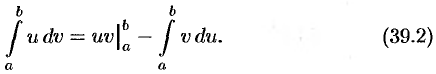
На отрезке  имеет место равенстве)
имеет место равенстве) 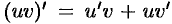 . Следовательно, функция
. Следовательно, функция 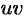 есть первообразная для непрерывной функции
есть первообразная для непрерывной функции 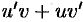 . Тогда по формуле Ньютона-Лейбница имеем:
. Тогда по формуле Ньютона-Лейбница имеем:
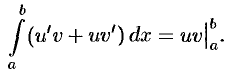
Следовательно,
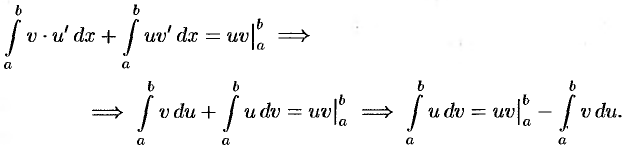
Формула (39.2) называется формулой интегрирования по частям для определенного интеграла.
Пример №39.2.
Вычислить 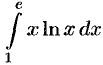 .
.
Решение:
Положим
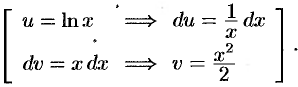
Применяя формулу (39.2), получаем
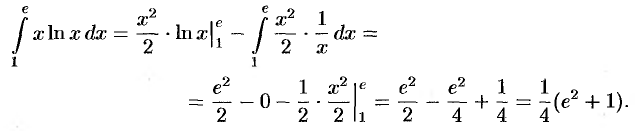
Дополнительный пример №39.3.
Дополнительная лекция: Интегрирование четных и нечетных функций в симметричных пределах
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Геометрический и физический смысл определенного интеграла |
| Основные свойства определенного интеграла |
| Интеграл с бесконечным промежутком интегрирования |
| Интеграл от разрывной функции |

