Оглавление:
Интегралы типа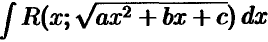 
Здесь подынтегральная функция есть рациональная функция относительно 
и 
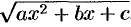. Выделив под радикалом полный квадрат и сделав подстановку 
, интегралы указанного типа приводятся к интегралам уже рассмотренного типа, т. е. к интегралам типа 
. Эти интегралы можно вычислить с помощью соответствующих тригонометрических подстановок.
Пример №33.7.
Найти интеграл 
.
Решение:
Так как 
, то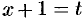 
, 
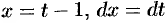. Поэтому 
. Положим 
. Тогда
Замечание: Интеграл типа 
целесообразно находить с помощью подстановки 
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Дробно-линейная подстановка |
| Тригонометрическая подстановка |
| Интегрирование дифференциального бинома |
| «Берущиеся» и «Неберущиеся» интегралы |
