Оглавление:
Дробно-линейная подстановка
Интегралы типа 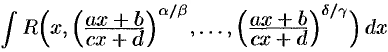 , где
, где 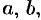
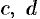 — действительные числа,
— действительные числа,  — натуральные числа, сводятся к интегралам от рациональной функции путем подстановки
— натуральные числа, сводятся к интегралам от рациональной функции путем подстановки 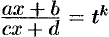 , где
, где 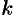 — наименьшее общее кратное знаменателей дробей
— наименьшее общее кратное знаменателей дробей 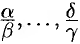 .
.
Действительно, из подстановки 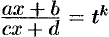 следует, что
следует, что 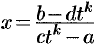 и
и 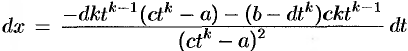 , т.е.
, т.е.  и
и 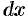 выражаются через рациональные функции от
выражаются через рациональные функции от  . При этом и каждая степень дроби
. При этом и каждая степень дроби 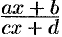 выражается через рациональную функцию от
выражается через рациональную функцию от  .
.
Пример №33.4.
Найти интеграл 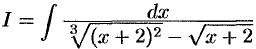 .
.
Решение:
Наименьшее общее кратное знаменателей дробей 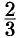 и
и 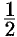 есть 6. Поэтому полагаем
есть 6. Поэтому полагаем 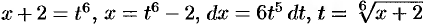 .
.
Следовательно
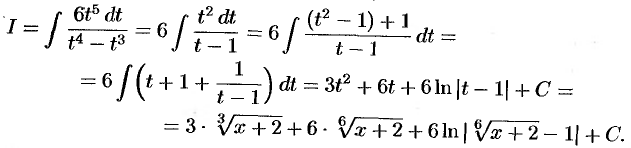
Дополнительный пример №33.5.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Использование тригонометрических преобразований |
| Квадратичные иррациональности |
| Тригонометрическая подстановка |
| Интегралы типа r x (ax^2+bx+c) dx |

