Оглавление:
Интегралы типа 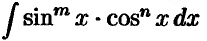
Для нахождения таких интегралов используются следующие приемы:
1) подстановка 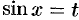 , если
, если  — целое положительное нечетное число;
— целое положительное нечетное число;
2) подстановка 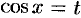 , если
, если 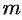 — целое положительное нечетное число;
— целое положительное нечетное число;
3) формулы понижения порядка: 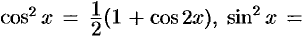
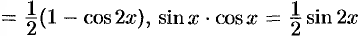 , если
, если 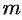 и
и  — целые неотрицательные четные числа;
— целые неотрицательные четные числа;
4) подстановка 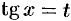 , если
, если 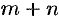 — есть четное отрицательное целое число.
— есть четное отрицательное целое число.
Пример №32.3.
Найти интеграл 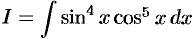 .
.
Решение:
Применим подстановку 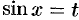 . Тогда
. Тогда 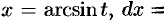
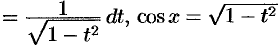 и
и
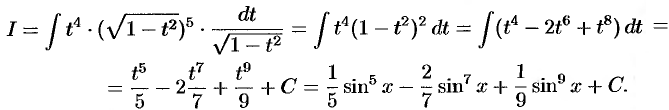
Дополнительные примеры:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Интегрирование рациональных дробей |
| Универсальная тригонометрическая подстановка |
| Использование тригонометрических преобразований |
| Квадратичные иррациональности |

