Оглавление:
Метод интегрирования подстановкой (заменой переменной)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т. е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся (в случае «удачной» подстановки). Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл 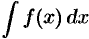 . Сделаем подстановку
. Сделаем подстановку 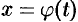 , где
, где 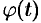 — функция, имеющая непрерывную производную.
— функция, имеющая непрерывную производную.
Тогда 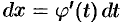 и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой
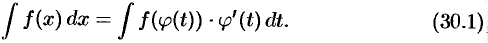
Формула (30.1) также называется формулой замены переменных в неопределенном интеграле. После нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования  назад к переменной
назад к переменной  .
.
Иногда целесообразно подбирать подстановку в виде 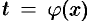 , тогда
, тогда 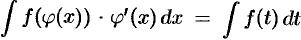 , где
, где 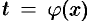 . Другими словами, формулу (30.1) можно применять справа налево.
. Другими словами, формулу (30.1) можно применять справа налево.
Пример №30.1.
Найти 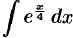 .
.
Решение:
Положим 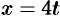 , тогда
, тогда 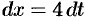 . Следовательно,
. Следовательно,
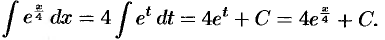
Дополнительные примеры:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Свойства неопределенного интеграла |
| Метод непосредственного интегрирования |
| Метод интегрирования по частям |
| Понятия о рациональных функциях |

